浙江省衢州第二中学2023-2024学年高一下学期5月阶段检测数学试题
浙江
高一
期中
2024-06-17
393次
整体难度:
容易
考查范围:
计数原理与概率统计、复数、三角函数与解三角形、空间向量与立体几何、函数与导数、等式与不等式、平面向量、平面解析几何
一、单选题 添加题型下试题
| A.133石 | B.168石 | C.337石 | D.1364石 |
 的边长为1,它是水平放置的一个平面图形的直观图,则原图形面积是( )
的边长为1,它是水平放置的一个平面图形的直观图,则原图形面积是( )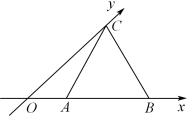
A. | B. | C.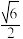 | D.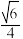 |
【知识点】 正弦定理解三角形解读 斜二测画法中有关量的计算
 这
这 个数据构成,记这组数据的平均数为
个数据构成,记这组数据的平均数为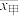 ,方差为
,方差为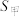 ;乙组数据由
;乙组数据由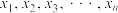 ,
,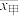 这
这 数据构成,记这组数据的平均数为
数据构成,记这组数据的平均数为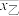 ,方差为
,方差为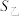 ,则( )
,则( )A. , , | B. , ,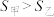 |
C. , , | D. , ,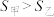 |
【知识点】 计算几个数的平均数解读 计算几个数据的极差、方差、标准差
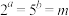 ,且
,且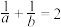 ,则
,则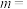 ( )
( )A.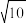 | B.10 | C.20 | D.100 |
【知识点】 指数式与对数式的互化 对数的运算 运用换底公式化简计算
 满足
满足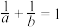 ,则
,则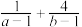 的最小值为( )
的最小值为( )| A.4 | B.6 | C.9 | D.16 |
【知识点】 基本不等式求和的最小值解读 条件等式求最值解读
A.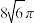 | B.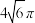 | C.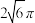 | D. |
【知识点】 球的表面积的有关计算
二、多选题 添加题型下试题
 ,则下列关于函数
,则下列关于函数 的结论中,正确的是( )
的结论中,正确的是( )| A.最大值为1 | B.图象关于直线 对称 对称 |
| C.既是奇函数又是周期函数 | D.图象关于点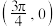 中心对称 中心对称 |
 ,则( )
,则( )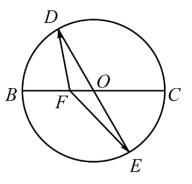
A. |
B.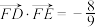 |
C.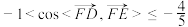 |
D.满足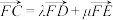 的实数 的实数 与 与 的和为定值4 的和为定值4 |
 的棱长为2,点
的棱长为2,点 为平面
为平面 内一动点,则下列说法正确的是( )
内一动点,则下列说法正确的是( )A.若点 在棱 在棱 上运动,则 上运动,则 的最小值为 的最小值为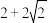 |
B.若点 是棱 是棱 的中点,则平面 的中点,则平面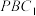 截正方体所得截面的周长为 截正方体所得截面的周长为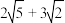 |
C.若点 满足 满足 ,则动点 ,则动点 的轨迹是一条直线 的轨迹是一条直线 |
D.若点 在直线 在直线 上运动,则 上运动,则 到棱 到棱 的最小距离为 的最小距离为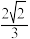 |
三、填空题 添加题型下试题
 是第三象限角,且
是第三象限角,且 ,则
,则
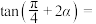
 中,点
中,点 分别是棱
分别是棱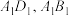 的中点,
的中点, 是侧面正方形
是侧面正方形 内一点(含边界),若
内一点(含边界),若 平面
平面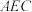 ,则线段
,则线段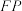 长度的取值范围是
长度的取值范围是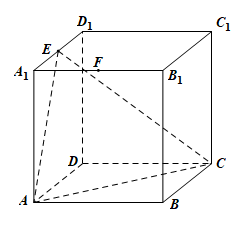
【知识点】 证明面面平行 由线面平行求线段长度
 为
为 的重心,满足
的重心,满足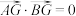 .若
.若 ,则实数
,则实数 的值为
的值为【知识点】 用和、差角的正弦公式化简、求值解读 余弦定理解三角形解读
四、解答题 添加题型下试题
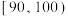 ,
, ,
,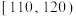 ,
, ,
,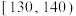 ,
,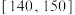 ,后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
,后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: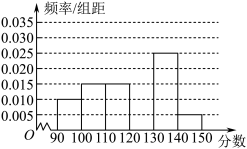
 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;(2)估计本次考试的平均分、中位数及
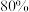 分位数的值.
分位数的值.
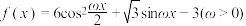 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点, 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形.
为正三角形.
 的值及函数
的值及函数 的值域;
的值域;(2)若
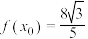 ,且
,且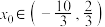 ,求
,求 的值.
的值.
【知识点】 由图象确定正(余)弦型函数解析式解读 辅助角公式解读
 中,内角
中,内角 ,
, ,
, 所对的边长分别为
所对的边长分别为 ,
, ,
, ,且满足
,且满足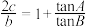 .
.(1)求角
 ;
;(2)角
 的内角平分线交
的内角平分线交 于点
于点 ,若
,若 ,
,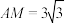 ,求
,求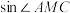 .
.
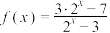 ,
, .
.(1)当
 时,求函数
时,求函数 的值城
的值城(2)若关于
 的方程
的方程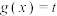 有两个不等根
有两个不等根 ,求
,求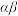 的值;
的值;(3)是否存在实数
 ,使得对任意
,使得对任意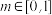 ,关于
,关于 的方程
的方程 在区间
在区间 上
上 ,
, ,
, ,若存在,求出实数
,若存在,求出实数 与
与 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【知识点】 求指数型复合函数的值域 简单的对数方程 根据函数零点的个数求参数范围
试卷分析
导出试卷题型(共 19题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 总体与样本 | |
| 2 | 0.94 | 求复数的实部与虚部 复数的除法运算 | |
| 3 | 0.85 | 正弦定理解三角形 斜二测画法中有关量的计算 | |
| 4 | 0.65 | 计算几个数的平均数 计算几个数据的极差、方差、标准差 | |
| 5 | 0.85 | 指数式与对数式的互化 对数的运算 运用换底公式化简计算 | |
| 6 | 0.85 | 三角函数的化简、求值——同角三角函数基本关系 诱导公式二、三、四 诱导公式五、六 | |
| 7 | 0.65 | 基本不等式求和的最小值 条件等式求最值 | |
| 8 | 0.65 | 球的表面积的有关计算 | |
| 二、多选题 | |||
| 9 | 0.65 | 函数奇偶性的定义与判断 求含sinx(型)函数的值域和最值 求cosx(型)函数的对称轴及对称中心 | |
| 10 | 0.65 | 二倍角的余弦公式 向量的线性运算的几何应用 数量积的运算律 向量夹角的计算 | |
| 11 | 0.65 | 由平面的基本性质作截面图形 线面垂直证明线线垂直 点到直线距离的向量求法 立体几何中的轨迹问题 | 2个答案 |
| 三、填空题 | |||
| 12 | 0.85 | 已知正(余)弦求余(正)弦 三角函数的化简、求值——诱导公式 二倍角的余弦公式 二倍角的正切公式 | 双空题 |
| 13 | 0.85 | 证明面面平行 由线面平行求线段长度 | 单空题 |
| 14 | 0.4 | 用和、差角的正弦公式化简、求值 余弦定理解三角形 | 单空题 |
| 四、解答题 | |||
| 15 | 0.65 | 补全频率分布直方图 由频率分布直方图估计中位数 由频率分布直方图估计平均数 总体百分位数的估计 | 应用题 |
| 16 | 0.65 | 由图象确定正(余)弦型函数解析式 辅助角公式 | 问答题 |
| 17 | 0.65 | 正弦定理解三角形 正弦定理边角互化的应用 三角形面积公式及其应用 余弦定理解三角形 | 问答题 |
| 18 | 0.65 | 面面垂直证线面垂直 线面角的向量求法 面面角的向量求法 | 证明题 |
| 19 | 0.65 | 求指数型复合函数的值域 简单的对数方程 根据函数零点的个数求参数范围 | 问答题 |

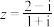 ,则复数
,则复数 的虚部为(
的虚部为(
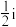
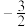
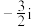
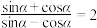 ,则
,则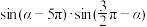 的值为(
的值为(

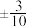
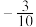
 中,
中,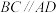 ,
, ,平面
,平面 平面
平面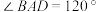 ,且
,且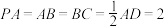 .
.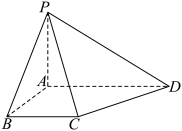
 平面
平面 与平面
与平面 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值.


