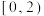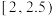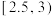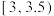北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
北京
高二
阶段练习
2024-06-28
914次
整体难度:
容易
考查范围:
计数原理与概率统计、数列、平面解析几何、函数与导数、空间向量与立体几何、推理与证明、集合与常用逻辑用语
北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
北京
高二
阶段练习
2024-06-28
914次
整体难度:
容易
考查范围:
计数原理与概率统计、数列、平面解析几何、函数与导数、空间向量与立体几何、推理与证明、集合与常用逻辑用语
一、单选题 添加题型下试题
单选题
|
容易(0.94)
名校
您最近一年使用:0次
2024-05-29更新
|
695次组卷
|
7卷引用:重庆市第四十九中学校、江津第二中学校等九校2023-2024学年高二下学期5月联考数学试题
单选题
|
容易(0.94)
名校
2. 已知等比数列 满足
满足 ,
, ,则
,则 等于( )
等于( )
 满足
满足 ,
, ,则
,则 等于( )
等于( )A. | B.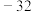 | C.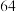 | D.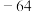 |
【知识点】 写出等比数列的通项公式 利用等比数列的通项公式求数列中的项
您最近一年使用:0次
2021-01-20更新
|
1665次组卷
|
7卷引用:北京市丰台区2020-2021学年高二上学期期末练习数学试题
单选题
|
较易(0.85)
名校
3. 已知离散型随机变量X的分布列如下:
则其数学期望E(X)等于( )
| X | 1 | 3 | 5 |
| P | 0.5 | m | 0.2 |
| A.1 | B.0.6 | C.2+3m | D.2.4 |
您最近一年使用:0次
2022-05-18更新
|
1061次组卷
|
9卷引用:山东省滨州市2021-2022学年高二上学期期中数学试题
山东省滨州市2021-2022学年高二上学期期中数学试题陕西省西北农林科技大学附属中学2021-2022学年高二下学期期末理科数学试题广东省佛山市南海区狮山高级中学2021-2022学年高二下学期第二次大测数学试题第六章 概率 章末测评卷甘肃省兰州市等4地2022届高三一模理科数学试题新疆柯坪县柯坪湖州国庆中学2023届高三上学期期末考试数学(理)试题(已下线)7.2离散型随机变量及其分布列 (分层作业)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题黑龙江省牡丹江市海林市朝鲜族中学2023-2024学年高二下学期第二次月考数学试卷
单选题
|
较易(0.85)
您最近一年使用:0次
2023-06-28更新
|
510次组卷
|
5卷引用:湖北省十堰市2022-2023学年高二下学期6月期末数学试题
单选题
|
较易(0.85)
名校
5. 假设某市场供应的灯泡中,甲厂产品占60%,乙厂产品占40%,甲厂产品的合格率是90%,乙厂产品的合格率是80%.在该市场中随机购买一个灯泡,是合格品的概率为( )
| A.84% | B.85% | C.86% | D.87% |
【知识点】 利用全概率公式求概率
您最近一年使用:0次
2022-05-04更新
|
765次组卷
|
3卷引用:北京师范大学附属实验中学2021-2022学年高二下学期期中数学试题
北京师范大学附属实验中学2021-2022学年高二下学期期中数学试题(已下线)7.1.1条件概率7.1.2全概率公式 第二课 归纳核心考点北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
单选题
|
容易(0.94)
名校
6. 若抛物线 的焦点到直线
的焦点到直线 的距离为4,则
的距离为4,则 的值为( )
的值为( )
 的焦点到直线
的焦点到直线 的距离为4,则
的距离为4,则 的值为( )
的值为( )| A.1 | B.2 | C.4 | D.8 |
【知识点】 根据抛物线方程求焦点或准线
您最近一年使用:0次
2024-05-13更新
|
1210次组卷
|
5卷引用:山东省烟台市2024年高考适应性练习(二模)数学试题
单选题
|
适中(0.65)
名校
解题方法
7. 甲、乙两人独立地破译一份密码,已知两人能破译的概率分别是 ,
, ,则( )
,则( )
 ,
, ,则( )
,则( )A.两人都成功破译的概率为 | B.两人都成功破译的概率为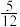 |
C.密码被成功破译的概率为 | D.密码被成功破译的概率为 |
【知识点】 互斥事件的概率加法公式解读 独立事件的乘法公式解读
您最近一年使用:0次
2022-02-10更新
|
880次组卷
|
4卷引用:武汉市四校联合体2021-2022学年高二上学期期中联考数学试题
武汉市四校联合体2021-2022学年高二上学期期中联考数学试题(已下线)第03讲 互斥事件和独立事件-【帮课堂】2021-2022学年高一数学同步精品讲义(苏教版2019必修第二册)湖北省随州市曾都区第一中学2022-2023学年高二上学期开学测试数学试题北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
单选题
|
适中(0.65)
名校
您最近一年使用:0次
2019-12-16更新
|
513次组卷
|
3卷引用:安徽省五校(怀远一中、蒙城一中、淮南一中、颍上一中、淮南一中、涡阳一中)2019-2020学年高三联考数学(理)试题
单选题
|
适中(0.65)
名校
解题方法
9. 有一支医疗小队由3名医生和6名护士组成,平均分配到三家医院,每家医院分到医生1名和护士2名.其中护士甲和护士乙必须分到同一家医院,则不同的分配方法有( )种.
| A.36 | B.72 | C.108 | D.144 |
您最近一年使用:0次
2024-06-28更新
|
753次组卷
|
5卷引用:河北省石家庄二十四中2023-2024学年高二下学期第一次月考数学试题
河北省石家庄二十四中2023-2024学年高二下学期第一次月考数学试题(已下线)专题01 排列组合及其应用常考题型归类--高二期末考点大串讲(人教B版2019选择性必修第二册)(已下线)核心考点4 排列组合和二项式定理 专题讲解 B提升卷 (高二期末考试必考的10大核心考点)(已下线)专题9 排列组合的实际应用问题【讲】(高二期末压轴专项)北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
单选题
|
适中(0.65)
名校
解题方法
10. 某制造商制造并出售球形瓶装的某种饮料,一个瓶子的制造成本是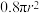 分,其中
分,其中 (单位:
(单位: )是瓶子的半径.已知每出售
)是瓶子的半径.已知每出售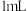 的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为
的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为 ,则使得每瓶饮料的利润最大时的瓶子的半径为( )
,则使得每瓶饮料的利润最大时的瓶子的半径为( )
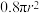 分,其中
分,其中 (单位:
(单位: )是瓶子的半径.已知每出售
)是瓶子的半径.已知每出售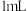 的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为
的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为 ,则使得每瓶饮料的利润最大时的瓶子的半径为( )
,则使得每瓶饮料的利润最大时的瓶子的半径为( )A.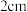 | B.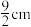 | C.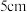 | D. |
您最近一年使用:0次
2023-07-08更新
|
402次组卷
|
5卷引用:广东省汕尾市2022-2023学年高二下学期期末数学试题
广东省汕尾市2022-2023学年高二下学期期末数学试题(已下线)第10讲:导数期末题型突破(单调性、不等式、零点、恒成立)广东省东莞市常平中学2023-2024学年高二下学期3月阶段检测数学试题(已下线)必考考点2 导数几何意义和函数的单调性、极值 专题讲解 (期末考试必考的10大核心考点) 北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
二、填空题 添加题型下试题
填空题-单空题
|
容易(0.94)
名校
解题方法
11. 若随机变量X服从二项分布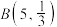 ,则
,则
______ .
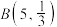 ,则
,则
【知识点】 利用二项分布求分布列解读
您最近一年使用:0次
2022-09-07更新
|
1352次组卷
|
7卷引用:沪教版(2020) 选修第二册 单元训练 第7章 概率初步(续)—常用分布(A卷)
沪教版(2020) 选修第二册 单元训练 第7章 概率初步(续)—常用分布(A卷)(已下线)专题2二项分布运算(基础版)(已下线)第08讲 二项分布与超几何分布、正态分布 (高频考点,精讲)-1(已下线)7.4.1 二项分布(分层作业)河南省焦作市宇华实验学校2023-2024学年高二上学期期末拔高数学试题(二)(已下线)专题03 随机变量及其分布列-2北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
填空题-单空题
|
较易(0.85)
名校
解题方法
您最近一年使用:0次
2018-07-19更新
|
695次组卷
|
4卷引用:【全国校级联考】辽宁省实验中学等五校2017-2018学年高二下学期期末考试数学(理)试题
填空题-单空题
|
适中(0.65)
名校
您最近一年使用:0次
2020-01-08更新
|
712次组卷
|
7卷引用:四川省广安遂宁资阳等七市2019-2020学年高三上学期第一次诊断性考试数学(理)试题
填空题-单空题
|
适中(0.65)
名校
解题方法
您最近一年使用:0次
2023-01-03更新
|
502次组卷
|
4卷引用:沪教版(2020) 选修第二册 堂堂清 第6章 6.3(3)组合(组合的应用)
沪教版(2020) 选修第二册 堂堂清 第6章 6.3(3)组合(组合的应用)(已下线)河南省南阳市2022-2023学年高三上学期期末数学(理)试题变式题11-15(已下线)第六章 计数原理 全章总结 (精讲)(3)北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
填空题-单空题
|
适中(0.65)
名校
15. 已知数列 满足
满足 ,
,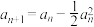 .给出下列四个结论:
.给出下列四个结论:
①数列 每一项
每一项 都满足
都满足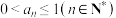 ;
;
②数列 是递减数列;
是递减数列;
③数列 的前n项和
的前n项和 ;
;
④数列 每一项都满足
每一项都满足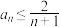 成立.
成立.
其中,所有正确结论的序号是__________ .
 满足
满足 ,
,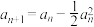 .给出下列四个结论:
.给出下列四个结论:①数列
 每一项
每一项 都满足
都满足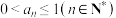 ;
;②数列
 是递减数列;
是递减数列;③数列
 的前n项和
的前n项和 ;
;④数列
 每一项都满足
每一项都满足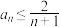 成立.
成立.其中,所有正确结论的序号是
您最近一年使用:0次
2024-05-23更新
|
279次组卷
|
3卷引用:北京市大峪中学2023-2024学年高二下学期期中调研数学试题
北京市大峪中学2023-2024学年高二下学期期中调研数学试题北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题(已下线)高二下学期期末考试01(范围:选修部分)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
三、解答题 添加题型下试题
解答题-应用题
|
较易(0.85)
名校
16. 某校为了解高二学生每天的作业完成时长,在该校高二学生中随机选取了100人,对他们每天完成各科作业的总时长进行了调研,结果如下表所示:
用表格中的频率估计概率,且每个学生完成各科作业时互不影响,
(1)从该校高二学生中随机选取1人,估计该生可以在3小时内完成各科作业的概率;
(2)从样本“完成各科作业的总时长在2.5小时内”的学生中随机选取3人,其中共有X人可以在2小时内完成各科作业,求X的分布列和数学期望;
(3)从该校高二学生(学生人数较多)中随机选取3人,其中共有 人可以在3小时内完成各科作业,
人可以在3小时内完成各科作业, 人在3小时及以上完成各科作业,试写出数学期望
人在3小时及以上完成各科作业,试写出数学期望 ,
, 并比较其大小关系.
并比较其大小关系.
时长t(小时) |
|
|
|
|
|
人数 | 3 | 4 | 33 | 42 | 18 |
(1)从该校高二学生中随机选取1人,估计该生可以在3小时内完成各科作业的概率;
(2)从样本“完成各科作业的总时长在2.5小时内”的学生中随机选取3人,其中共有X人可以在2小时内完成各科作业,求X的分布列和数学期望;
(3)从该校高二学生(学生人数较多)中随机选取3人,其中共有
 人可以在3小时内完成各科作业,
人可以在3小时内完成各科作业, 人在3小时及以上完成各科作业,试写出数学期望
人在3小时及以上完成各科作业,试写出数学期望 ,
, 并比较其大小关系.
并比较其大小关系.
您最近一年使用:0次
2024-05-21更新
|
916次组卷
|
5卷引用:湖北省云学名校联盟2023-2024学年高二下学期5月联考数学试题A卷
湖北省云学名校联盟2023-2024学年高二下学期5月联考数学试题A卷湖北省云学名校联盟2023-2024学年高二下学期5月联考数学试题B卷(已下线)高二数学下学期期末模拟--高二期末考点大串讲(苏教版2019选择性必修第二册)北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题安徽省合肥市第一中学瑶海校区2023-2024学年高二下学期数学素质拓展训练(五)
解答题-问答题
|
较难(0.4)
名校
17. 已知函数 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求 、
、 的值:
的值:
(2)求函数 的单调区间;
的单调区间;
(3)令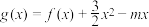 ,若函数
,若函数 的极小值小于
的极小值小于 ,求
,求 的取值范围.
的取值范围.
 在点
在点 处的切线方程为
处的切线方程为 .
.(1)求
 、
、 的值:
的值:(2)求函数
 的单调区间;
的单调区间;(3)令
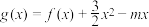 ,若函数
,若函数 的极小值小于
的极小值小于 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-08-02更新
|
1073次组卷
|
4卷引用:北京市清华附中2022-2023学年高二下学期期末数学试题
北京市清华附中2022-2023学年高二下学期期末数学试题(已下线)第09讲:一元函数的导数及其应用 (必刷7大考题+7大题型) -2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019)【北京专用】专题11导数及其应用(第三部分)-高二上学期名校期末好题汇编北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
解答题-证明题
|
较难(0.4)
名校
解题方法
18. 设A是正整数集的一个非空子集,如果对于任意 ,都有
,都有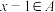 或
或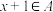 ,则称A为自邻集.记集合
,则称A为自邻集.记集合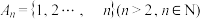 的所有子集中的自邻集的个数为
的所有子集中的自邻集的个数为 .
.
(1)直接写出 的所有自邻集;
的所有自邻集;
(2)若 为偶数且
为偶数且 ,求证:
,求证: 的所有含5个元素的子集中,自邻集的个数是偶数;
的所有含5个元素的子集中,自邻集的个数是偶数;
(3)若 ,求证:
,求证: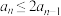 .
.
 ,都有
,都有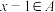 或
或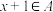 ,则称A为自邻集.记集合
,则称A为自邻集.记集合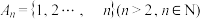 的所有子集中的自邻集的个数为
的所有子集中的自邻集的个数为 .
.(1)直接写出
 的所有自邻集;
的所有自邻集;(2)若
 为偶数且
为偶数且 ,求证:
,求证: 的所有含5个元素的子集中,自邻集的个数是偶数;
的所有含5个元素的子集中,自邻集的个数是偶数;(3)若
 ,求证:
,求证: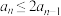 .
.
【知识点】 判断集合的子集(真子集)的个数 求集合的子集(真子集) 集合新定义
您最近一年使用:0次
2023-05-28更新
|
1163次组卷
|
13卷引用:北京市西城区2021届高三5月二模数学试题
北京市西城区2021届高三5月二模数学试题北京市第五十七中学2021-2022学年高二上学期期中检测数学试题北京市第二十中学2022-2023学年高二上学期12月月考数学试题北京一零一中学2023届高三下学期数学统练四试题北京卷专题02集合(解答题)北京市第一0一中学2022-2023学年高三下学期统练数学试卷(四)(已下线)高一上学期第一次月考解答题压轴题50题专练-举一反三系列北京市北京师范大学第二附属中学2023-2024学年高二上学期期中测试数学试题北京市东城区景山学校2024届高三上学期12月月考数学试题北京市第二中学2023-2024学年高二上学期12月第二学段考试数学试卷(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)(已下线)拔高点突破01 集合背景下的新定义压轴解答题(四大题型)北京市中国人民大学附属中学2023-2024学年高二下学期数学统练4试题
试卷分析
导出
整体难度:适中
考查范围:计数原理与概率统计、数列、平面解析几何、函数与导数、空间向量与立体几何、推理与证明、集合与常用逻辑用语
试卷题型(共 18题)
题型
数量
单选题
10
填空题
5
解答题
3
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 分类加法计数原理 | |
| 2 | 0.94 | 写出等比数列的通项公式 利用等比数列的通项公式求数列中的项 | |
| 3 | 0.85 | 利用随机变量分布列的性质解题 求离散型随机变量的均值 | |
| 4 | 0.85 | 方差的性质 二项分布的方差 | |
| 5 | 0.85 | 利用全概率公式求概率 | |
| 6 | 0.94 | 根据抛物线方程求焦点或准线 | |
| 7 | 0.65 | 互斥事件的概率加法公式 独立事件的乘法公式 | |
| 8 | 0.65 | 等比数列的单调性 前n项和与通项关系 | |
| 9 | 0.65 | 分组分配问题 | |
| 10 | 0.65 | 利润最大问题 球的体积的有关计算 | |
| 二、填空题 | |||
| 11 | 0.94 | 利用二项分布求分布列 | 单空题 |
| 12 | 0.85 | 计算条件概率 | 单空题 |
| 13 | 0.65 | 独立事件的乘法公式 | 单空题 |
| 14 | 0.65 | 分组分配问题 | 单空题 |
| 15 | 0.65 | 判断数列的增减性 由递推数列研究数列的有关性质 裂项相消法求和 数学归纳法证明数列问题 | 单空题 |
| 三、解答题 | |||
| 16 | 0.85 | 计算古典概型问题的概率 写出简单离散型随机变量分布列 二项分布的均值 | 应用题 |
| 17 | 0.4 | 已知切线(斜率)求参数 利用导数求函数的单调区间(不含参) 求已知函数的极值 根据极值求参数 | 问答题 |
| 18 | 0.4 | 判断集合的子集(真子集)的个数 求集合的子集(真子集) 集合新定义 | 证明题 |

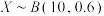 ,则
,则 (
( 的公比为
的公比为 ,前
,前 ,则“
,则“ ”是“
”是“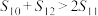 ”的
”的 ,则由此估计甲获得冠军的概率为
,则由此估计甲获得冠军的概率为