名校
解题方法
1 . 青岛胶东国际机场的显著特点之一是弯曲曲线的运用,衡量曲线弯曲程度的重要指标是曲率.考察图所示的光滑曲线 上的曲线段
上的曲线段 ,其弧长为
,其弧长为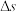 ,当动点从A沿曲线段
,当动点从A沿曲线段 运动到B点时,A点的切线
运动到B点时,A点的切线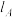 也随着转动到B点的切线
也随着转动到B点的切线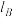 ,记这两条切线之间的夹角为
,记这两条切线之间的夹角为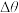 (它等于
(它等于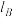 的倾斜角与
的倾斜角与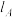 的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义
的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义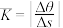 为曲线段
为曲线段 的平均曲率;显然当B越接近A,即
的平均曲率;显然当B越接近A,即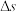 越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义曲线
越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义曲线 在点
在点 处的曲率计算公式为
处的曲率计算公式为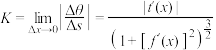 ,其中
,其中 .
. 的圆弧的平均曲率;
的圆弧的平均曲率;
(2)已知函数 ,求曲线
,求曲线 的曲率的最大值;
的曲率的最大值;
(3)已知函数 ,若
,若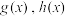 曲率为0时x的最小值分别为
曲率为0时x的最小值分别为 ,求证:
,求证: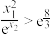 .
.
 上的曲线段
上的曲线段 ,其弧长为
,其弧长为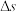 ,当动点从A沿曲线段
,当动点从A沿曲线段 运动到B点时,A点的切线
运动到B点时,A点的切线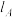 也随着转动到B点的切线
也随着转动到B点的切线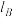 ,记这两条切线之间的夹角为
,记这两条切线之间的夹角为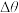 (它等于
(它等于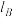 的倾斜角与
的倾斜角与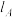 的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义
的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义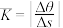 为曲线段
为曲线段 的平均曲率;显然当B越接近A,即
的平均曲率;显然当B越接近A,即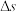 越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义曲线
越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义曲线 在点
在点 处的曲率计算公式为
处的曲率计算公式为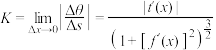 ,其中
,其中 .
.
 的圆弧的平均曲率;
的圆弧的平均曲率;(2)已知函数
 ,求曲线
,求曲线 的曲率的最大值;
的曲率的最大值;(3)已知函数
 ,若
,若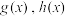 曲率为0时x的最小值分别为
曲率为0时x的最小值分别为 ,求证:
,求证: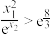 .
.
您最近一年使用:0次
2024-04-15更新
|
493次组卷
|
3卷引用:广东省江门市第一中学2023-2024学年高二下学期第一次段考数学试题
2 . 在平面直角坐标系 中,利用公式
中,利用公式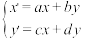 ①(其中
①(其中 ,
, ,
, ,
, 为常数),将点
为常数),将点 变换为点
变换为点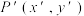 的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由
的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由 ,
, ,
, ,
, 组成的正方形数表
组成的正方形数表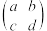 唯一确定,我们将
唯一确定,我们将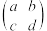 称为二阶矩阵,矩阵通常用大写英文字母
称为二阶矩阵,矩阵通常用大写英文字母 ,
, ,…表示.
,…表示. 中,将点
中,将点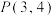 绕原点
绕原点 按逆时针旋转
按逆时针旋转 得到点
得到点 (到原点距离不变),求点
(到原点距离不变),求点 的坐标;
的坐标;
(2)如图,在平面直角坐标系 中,将点
中,将点 绕原点
绕原点 按逆时针旋转
按逆时针旋转 角得到点
角得到点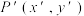 (到原点距离不变),求坐标变换公式及对应的二阶矩阵;
(到原点距离不变),求坐标变换公式及对应的二阶矩阵;
(3)向量 (称为行向量形式),也可以写成
(称为行向量形式),也可以写成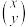 ,这种形式的向量称为列向量,线性变换坐标公式①可以表示为:
,这种形式的向量称为列向量,线性变换坐标公式①可以表示为: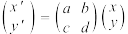 ,则称
,则称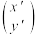 是二阶矩阵
是二阶矩阵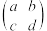 与向量
与向量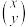 的乘积,设
的乘积,设 是一个二阶矩阵,
是一个二阶矩阵,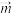 ,
, 是平面上的任意两个向量,求证:
是平面上的任意两个向量,求证: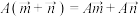 .
.
 中,利用公式
中,利用公式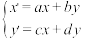 ①(其中
①(其中 ,
, ,
, ,
, 为常数),将点
为常数),将点 变换为点
变换为点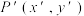 的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由
的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由 ,
, ,
, ,
, 组成的正方形数表
组成的正方形数表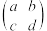 唯一确定,我们将
唯一确定,我们将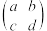 称为二阶矩阵,矩阵通常用大写英文字母
称为二阶矩阵,矩阵通常用大写英文字母 ,
, ,…表示.
,…表示.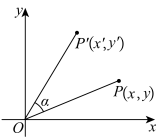
 中,将点
中,将点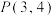 绕原点
绕原点 按逆时针旋转
按逆时针旋转 得到点
得到点 (到原点距离不变),求点
(到原点距离不变),求点 的坐标;
的坐标;(2)如图,在平面直角坐标系
 中,将点
中,将点 绕原点
绕原点 按逆时针旋转
按逆时针旋转 角得到点
角得到点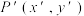 (到原点距离不变),求坐标变换公式及对应的二阶矩阵;
(到原点距离不变),求坐标变换公式及对应的二阶矩阵;(3)向量
 (称为行向量形式),也可以写成
(称为行向量形式),也可以写成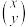 ,这种形式的向量称为列向量,线性变换坐标公式①可以表示为:
,这种形式的向量称为列向量,线性变换坐标公式①可以表示为: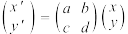 ,则称
,则称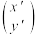 是二阶矩阵
是二阶矩阵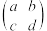 与向量
与向量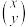 的乘积,设
的乘积,设 是一个二阶矩阵,
是一个二阶矩阵,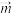 ,
, 是平面上的任意两个向量,求证:
是平面上的任意两个向量,求证: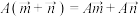 .
.
您最近一年使用:0次
2024-04-12更新
|
1972次组卷
|
7卷引用:湖南省湘楚名校2023-2024学年高二下学期5月月考数学试题
湖南省湘楚名校2023-2024学年高二下学期5月月考数学试题安徽省皖江名校联盟2024届高三下学期4月模拟数学试题(已下线)模块五 专题5 全真拔高模拟1(高一人教B版期中)(已下线)数学(新高考卷02,新题型结构)(已下线)模块五 专题5 全真拔高模拟1(苏教版期中研习高一)(已下线)压轴题02圆锥曲线压轴题17题型汇总-1黑龙江省实验中学2024届高三第四次模拟考试数学试题
3 . 已知函数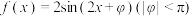 ,将函数
,将函数 向右平移
向右平移 个单位得到的图像关于
个单位得到的图像关于 轴对称且当
轴对称且当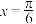 时,
时, 取得最大值.
取得最大值.
(1)求函数 的解析式:
的解析式:
(2)将函数 图象上所有的点向右平移
图象上所有的点向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,若
的图象,若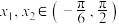 ,且
,且 ,求
,求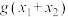 的值.
的值.
(3)方程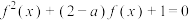 在
在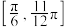 上有4个不相等的实数根,求实数
上有4个不相等的实数根,求实数 的取值范围.
的取值范围.
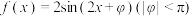 ,将函数
,将函数 向右平移
向右平移 个单位得到的图像关于
个单位得到的图像关于 轴对称且当
轴对称且当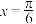 时,
时, 取得最大值.
取得最大值.(1)求函数
 的解析式:
的解析式:(2)将函数
 图象上所有的点向右平移
图象上所有的点向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,若
的图象,若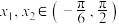 ,且
,且 ,求
,求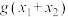 的值.
的值.(3)方程
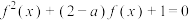 在
在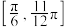 上有4个不相等的实数根,求实数
上有4个不相等的实数根,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-04-12更新
|
738次组卷
|
4卷引用:辽宁省沈阳市沈阳铁路实验中学2023-2024学年高一下学期4月月考数学试题
名校
解题方法
4 . 在 中,
中,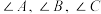 对应的边分别为
对应的边分别为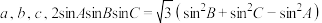
(1)求 ;
;
(2)奥古斯丁.路易斯.柯西(Augustin Louis Cauchy,1789年-1857年),法国著名数学家.柯西在数学领域有非常高的造诣.很多数学的定理和公式都以他的名字来命名,如柯西不等式、柯西积分公式.其中柯西不等式在解决不等式证明的有关问题中有着广泛的应用.
①用向量证明二维柯西不等式:
②已知三维分式型柯西不等式: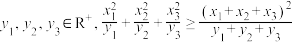 ,当且仅当
,当且仅当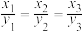 时等号成立.若
时等号成立.若 是
是 内一点,过
内一点,过 作
作 垂线,垂足分别为
垂线,垂足分别为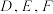 ,求
,求 的最小值.
的最小值.
 中,
中,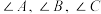 对应的边分别为
对应的边分别为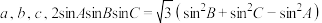
(1)求
 ;
;(2)奥古斯丁.路易斯.柯西(Augustin Louis Cauchy,1789年-1857年),法国著名数学家.柯西在数学领域有非常高的造诣.很多数学的定理和公式都以他的名字来命名,如柯西不等式、柯西积分公式.其中柯西不等式在解决不等式证明的有关问题中有着广泛的应用.
①用向量证明二维柯西不等式:

②已知三维分式型柯西不等式:
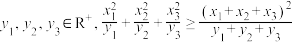 ,当且仅当
,当且仅当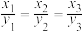 时等号成立.若
时等号成立.若 是
是 内一点,过
内一点,过 作
作 垂线,垂足分别为
垂线,垂足分别为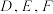 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024-04-11更新
|
427次组卷
|
5卷引用:福建省厦门双十中学2023-2024学年高一下学期4月月考数学试题
福建省厦门双十中学2023-2024学年高一下学期4月月考数学试题广东省佛山市南海区南海中学2023-2024学年高一下学期第二次阶段考试数学试题(已下线)模块五 专题6 全真拔高模拟2(高一人教B版期中 )(已下线)模块五 专题6 全真拔高模拟2(苏教版期中研习高一)(已下线)模块4 二模重组卷 第6套 复盘卷
2024高一下·上海·专题练习
解题方法
5 . 用 分别表示
分别表示 的三个内角
的三个内角 所对边的边长,
所对边的边长, 表示
表示 的外接圆半径.
的外接圆半径.
(1)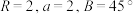 ,求
,求 的长;
的长;
(2)在 中,若
中,若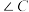 是钝角,求证:
是钝角,求证: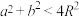 ;
;
(3)给定三个正实数 ,其中
,其中 ,问
,问 满足怎样的关系时,以
满足怎样的关系时,以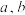 为边长,
为边长, 为外接圆半径的
为外接圆半径的 不存在,存在一个或存在两个(全等的三角形算作同一个)?在
不存在,存在一个或存在两个(全等的三角形算作同一个)?在 存在的情况下,用
存在的情况下,用 表示
表示 .
.
 分别表示
分别表示 的三个内角
的三个内角 所对边的边长,
所对边的边长, 表示
表示 的外接圆半径.
的外接圆半径.(1)
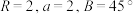 ,求
,求 的长;
的长;(2)在
 中,若
中,若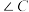 是钝角,求证:
是钝角,求证: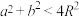 ;
;(3)给定三个正实数
 ,其中
,其中 ,问
,问 满足怎样的关系时,以
满足怎样的关系时,以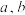 为边长,
为边长, 为外接圆半径的
为外接圆半径的 不存在,存在一个或存在两个(全等的三角形算作同一个)?在
不存在,存在一个或存在两个(全等的三角形算作同一个)?在 存在的情况下,用
存在的情况下,用 表示
表示 .
.
您最近一年使用:0次
名校
解题方法
6 . 已知 均为锐角,
均为锐角,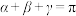 ,且
,且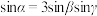 .
.
(1)若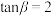 ,求
,求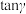 ;
;
(2)若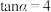 ,求
,求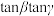 ;
;
(3)求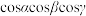 的最大值.
的最大值.
 均为锐角,
均为锐角,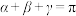 ,且
,且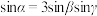 .
.(1)若
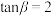 ,求
,求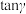 ;
;(2)若
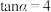 ,求
,求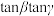 ;
;(3)求
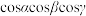 的最大值.
的最大值.
您最近一年使用:0次
名校
解题方法
7 . 定义非零向量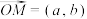 的(相伴函数)为
的(相伴函数)为 ,向量
,向量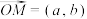 称为函数
称为函数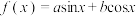 的“相伴向量”( 其中
的“相伴向量”( 其中 为坐标原点)
为坐标原点)
(1)求 的相伴向量;
的相伴向量;
(2)求(1)中函数 的“相伴向量”模的取值范围;
的“相伴向量”模的取值范围;
(3)已知点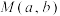 ,其中
,其中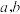 为锐角
为锐角 中角
中角 的对边.若角
的对边.若角 为
为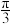 ,且向量
,且向量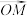 的“相伴函数”
的“相伴函数” 在
在 处取得最大值.求
处取得最大值.求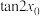 的取值范围.
的取值范围.
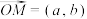 的(相伴函数)为
的(相伴函数)为 ,向量
,向量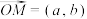 称为函数
称为函数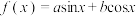 的“相伴向量”( 其中
的“相伴向量”( 其中 为坐标原点)
为坐标原点)(1)求
 的相伴向量;
的相伴向量;(2)求(1)中函数
 的“相伴向量”模的取值范围;
的“相伴向量”模的取值范围;(3)已知点
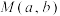 ,其中
,其中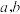 为锐角
为锐角 中角
中角 的对边.若角
的对边.若角 为
为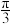 ,且向量
,且向量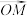 的“相伴函数”
的“相伴函数” 在
在 处取得最大值.求
处取得最大值.求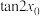 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
8 . 如图,现有一食品厂的占地区域为半圆形,直径 为AB的中点,
为AB的中点, 为OB的中点,点
为OB的中点,点 在BA的延长线上,且
在BA的延长线上,且 ,市政规划要求,在半圆弧上选取一点
,市政规划要求,在半圆弧上选取一点 ,各修建一条地下管道EC和ED通往C,D两点.
,各修建一条地下管道EC和ED通往C,D两点.
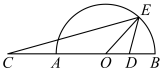
(1)设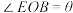 ,试将管道总长(即EC+ED)表示为
,试将管道总长(即EC+ED)表示为 的函数;
的函数;
(2)若修建管道EC的费用为10万元 ,修建管道ED的费用为20万元
,修建管道ED的费用为20万元 ,求修建管道的总费用的最大值.
,求修建管道的总费用的最大值.
 为AB的中点,
为AB的中点, 为OB的中点,点
为OB的中点,点 在BA的延长线上,且
在BA的延长线上,且 ,市政规划要求,在半圆弧上选取一点
,市政规划要求,在半圆弧上选取一点 ,各修建一条地下管道EC和ED通往C,D两点.
,各修建一条地下管道EC和ED通往C,D两点.
(1)设
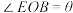 ,试将管道总长(即EC+ED)表示为
,试将管道总长(即EC+ED)表示为 的函数;
的函数;(2)若修建管道EC的费用为10万元
 ,修建管道ED的费用为20万元
,修建管道ED的费用为20万元 ,求修建管道的总费用的最大值.
,求修建管道的总费用的最大值.
您最近一年使用:0次
9 . 定义: 为实数
为实数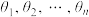 对
对 的“正弦方差”.
的“正弦方差”.
(1)若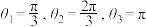 ,则实数
,则实数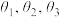 对
对 的“正弦方差”
的“正弦方差” 的值是否是与
的值是否是与 无关的定值,并证明你的结论
无关的定值,并证明你的结论
(2)若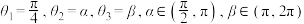 ,若实数
,若实数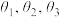 对
对 的“正弦方差”
的“正弦方差” 的值是与
的值是与 无关的定值,求
无关的定值,求 值.
值.
 为实数
为实数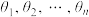 对
对 的“正弦方差”.
的“正弦方差”.(1)若
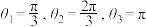 ,则实数
,则实数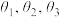 对
对 的“正弦方差”
的“正弦方差” 的值是否是与
的值是否是与 无关的定值,并证明你的结论
无关的定值,并证明你的结论(2)若
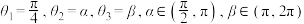 ,若实数
,若实数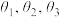 对
对 的“正弦方差”
的“正弦方差” 的值是与
的值是与 无关的定值,求
无关的定值,求 值.
值.
您最近一年使用:0次
名校
10 . 定义函数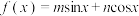 的“源向量”为
的“源向量”为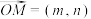 ,非零向量
,非零向量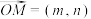 的“伴随函数”为
的“伴随函数”为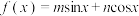 ,其中
,其中 为坐标原点.
为坐标原点.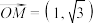 的“伴随函数”为
的“伴随函数”为 ,求
,求 在
在 的值域;
的值域;
(2)若函数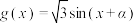 的“源向量”为
的“源向量”为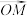 ,且以
,且以 为圆心,
为圆心,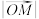 为半径的圆内切于正
为半径的圆内切于正 (顶点
(顶点 恰好在
恰好在 轴的正半轴上),求证:
轴的正半轴上),求证: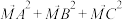 为定值;
为定值;
(3)在 中,角
中,角 的对边分别为
的对边分别为 ,若函数
,若函数 的“源向量”为
的“源向量”为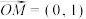 ,且已知
,且已知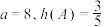 ,求
,求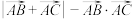 的取值范围.
的取值范围.
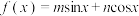 的“源向量”为
的“源向量”为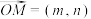 ,非零向量
,非零向量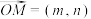 的“伴随函数”为
的“伴随函数”为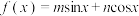 ,其中
,其中 为坐标原点.
为坐标原点.
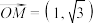 的“伴随函数”为
的“伴随函数”为 ,求
,求 在
在 的值域;
的值域;(2)若函数
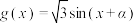 的“源向量”为
的“源向量”为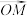 ,且以
,且以 为圆心,
为圆心,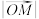 为半径的圆内切于正
为半径的圆内切于正 (顶点
(顶点 恰好在
恰好在 轴的正半轴上),求证:
轴的正半轴上),求证: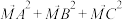 为定值;
为定值;(3)在
 中,角
中,角 的对边分别为
的对边分别为 ,若函数
,若函数 的“源向量”为
的“源向量”为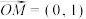 ,且已知
,且已知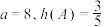 ,求
,求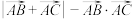 的取值范围.
的取值范围.
您最近一年使用:0次
2024-04-07更新
|
735次组卷
|
2卷引用:重庆市巴蜀中学校2023-2024学年高一下学期3月月考数学试题



