解题方法
1 . 如图,在直三棱柱 中,
中, 是等边三角形,
是等边三角形, ,D是棱AB的中点.
,D是棱AB的中点.
(1)证明.平面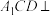 平面
平面 ;
;
(2)求AC与平面 所成线面角的正弦值
所成线面角的正弦值
 中,
中, 是等边三角形,
是等边三角形, ,D是棱AB的中点.
,D是棱AB的中点.
(1)证明.平面
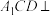 平面
平面 ;
;(2)求AC与平面
 所成线面角的正弦值
所成线面角的正弦值
您最近一年使用:0次
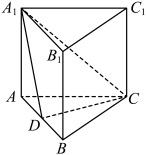
2 . 已知平行六面体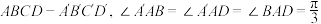 ,底面
,底面 为菱形,
为菱形, ,侧棱
,侧棱 .
.
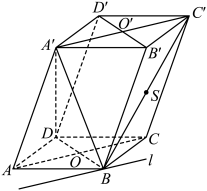
(1)证明:直线 平面
平面 ;
;
(2)设平面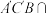 平面
平面 ,且二面角
,且二面角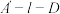 的平面角为
的平面角为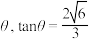 ,设
,设 点为线段
点为线段 的中点,求直线
的中点,求直线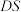 与平面
与平面 所成角的正弦值.
所成角的正弦值.
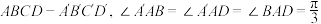 ,底面
,底面 为菱形,
为菱形, ,侧棱
,侧棱 .
.
(1)证明:直线
 平面
平面 ;
;(2)设平面
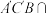 平面
平面 ,且二面角
,且二面角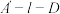 的平面角为
的平面角为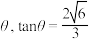 ,设
,设 点为线段
点为线段 的中点,求直线
的中点,求直线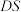 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-07-08更新
|
728次组卷
|
3卷引用:湖北省部分市州2022-2023学年高一下学期7月期末联考数学试题
湖北省部分市州2022-2023学年高一下学期7月期末联考数学试题(已下线)10.4 平面与平面间的位置关系(第2课时)(九大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)【人教A版(2019)】专题15立体几何与空间向量(第四部分)-高一下学期名校期末好题汇编
解题方法
3 . 如图,在正三棱台 中,
中,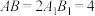 ,
, .
. .
.
(2)过 的平面α交
的平面α交 分别于
分别于 ,若
,若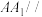 平面
平面 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中,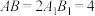 ,
, .
.
 .
.(2)过
 的平面α交
的平面α交 分别于
分别于 ,若
,若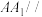 平面
平面 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-07-08更新
|
613次组卷
|
4卷引用:广东省清远市2022-2023学年高一下学期期末数学试题
名校
解题方法
4 . 如图,ABDC是平面四边形, 为正三角形,
为正三角形,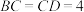 ,
, .将
.将 沿BC翻折,过点A作平面BCD的垂线,垂足为H.
沿BC翻折,过点A作平面BCD的垂线,垂足为H.
(2)若点H在BCD内部,且直线AB与平面ACD所成角的正弦值为 ,求二面角
,求二面角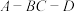 的余弦值.
的余弦值.
 为正三角形,
为正三角形,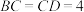 ,
, .将
.将 沿BC翻折,过点A作平面BCD的垂线,垂足为H.
沿BC翻折,过点A作平面BCD的垂线,垂足为H.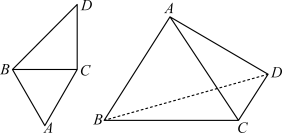
(2)若点H在BCD内部,且直线AB与平面ACD所成角的正弦值为
 ,求二面角
,求二面角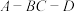 的余弦值.
的余弦值.
您最近一年使用:0次
2023-07-07更新
|
429次组卷
|
3卷引用:广东省江门市2022-2023学年高一下学期期末数学试题
名校
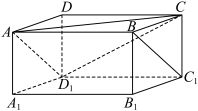
5 . 如图,直四棱柱 中,底面
中,底面 为矩形,且
为矩形,且
 与平面
与平面 所成的角的大小;
所成的角的大小;
(2)求二面角 的余弦值;
的余弦值;
(3)求直线 到平面
到平面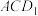 的距离.
的距离.
 中,底面
中,底面 为矩形,且
为矩形,且
 与平面
与平面 所成的角的大小;
所成的角的大小;(2)求二面角
 的余弦值;
的余弦值;(3)求直线
 到平面
到平面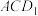 的距离.
的距离.
您最近一年使用:0次
2023-07-06更新
|
378次组卷
|
4卷引用:四川省遂宁市2022-2023学年高一下学期期末数学试题
四川省遂宁市2022-2023学年高一下学期期末数学试题(已下线)高一下学期期末复习解答题压轴题二十四大题型专练(2)-举一反三系列(人教A版2019必修第二册)(已下线)【高一模块二】类型5 以立体几何中的角度与距离计算为背景的解答题(A卷基础卷)新疆乌鲁木齐市第一中学2023-2024学年高一下学期期末考试数学试题
6 . 如图,在直三棱柱 中,
中, ,
, .
.

(1)设平面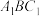 与平面
与平面 的交线为l,判断l与
的交线为l,判断l与 的位置关系,并证明;
的位置关系,并证明;
(2)若 与平面
与平面 所成的角为
所成的角为 ,求三棱锥
,求三棱锥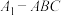 内切球的表面积S.
内切球的表面积S.
 中,
中, ,
, .
.
(1)设平面
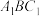 与平面
与平面 的交线为l,判断l与
的交线为l,判断l与 的位置关系,并证明;
的位置关系,并证明;(2)若
 与平面
与平面 所成的角为
所成的角为 ,求三棱锥
,求三棱锥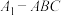 内切球的表面积S.
内切球的表面积S.
您最近一年使用:0次
7 . 如图,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 底面
底面 ,
, ,
, 为线段
为线段 的中点.
的中点.

(1)证明:
 平面
平面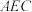 ;
;
(2)求 与平面
与平面 所成角的正切值.
所成角的正切值.
 中,底面
中,底面 为正方形,
为正方形, 底面
底面 ,
, ,
, 为线段
为线段 的中点.
的中点.
(1)证明:

 平面
平面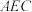 ;
;(2)求
 与平面
与平面 所成角的正切值.
所成角的正切值.
您最近一年使用:0次
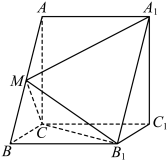
8 . 如图,在三棱柱 中,
中,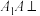 平面
平面 ,
, ,M是AB的中点,
,M是AB的中点, .
.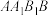 ;
;
(2)求直线 与平面
与平面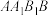 所成角的大小.
所成角的大小.
 中,
中,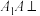 平面
平面 ,
, ,M是AB的中点,
,M是AB的中点, .
.
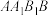 ;
;(2)求直线
 与平面
与平面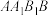 所成角的大小.
所成角的大小.
您最近一年使用:0次
2023-07-05更新
|
721次组卷
|
2卷引用:广东省广州市番禺区2022-2023学年高一下学期期末数学试题
解题方法
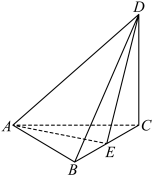
9 . 三棱锥 中,底面
中,底面 为正三角形,
为正三角形,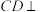 平面
平面 ,
, 为棱
为棱 的中点,且
的中点,且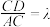 (
( 为正常数).
为正常数).
(1)若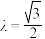 ,求二面角
,求二面角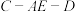 的大小;
的大小;
(2)记直线 和平面
和平面 所成角为
所成角为 ,试用常数
,试用常数 表示
表示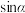 的值,并求
的值,并求 的取值范围.
的取值范围.
 中,底面
中,底面 为正三角形,
为正三角形,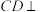 平面
平面 ,
, 为棱
为棱 的中点,且
的中点,且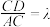 (
( 为正常数).
为正常数).
(1)若
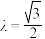 ,求二面角
,求二面角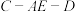 的大小;
的大小;(2)记直线
 和平面
和平面 所成角为
所成角为 ,试用常数
,试用常数 表示
表示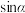 的值,并求
的值,并求 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
10 . 如图,直三棱柱 中,
中, ,且平面
,且平面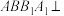 平面
平面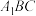 .
.

(1)求BC的长;
(2)求直线AC与平面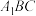 所成角的正弦值.
所成角的正弦值.
 中,
中, ,且平面
,且平面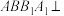 平面
平面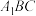 .
.
(1)求BC的长;
(2)求直线AC与平面
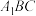 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次



