名校
解题方法
1 . 已知三棱锥 ,
,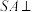 平面
平面 ,
, ,
,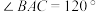 ,若三棱锥外接球的表面积为
,若三棱锥外接球的表面积为 ,则此三棱锥的体积为( )
,则此三棱锥的体积为( )
 ,
,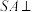 平面
平面 ,
, ,
,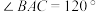 ,若三棱锥外接球的表面积为
,若三棱锥外接球的表面积为 ,则此三棱锥的体积为( )
,则此三棱锥的体积为( )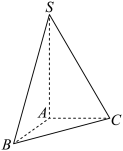
| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
名校
解题方法
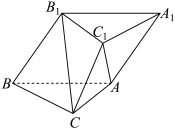
2 . 如图,在三棱柱 中,
中, ,四边形
,四边形 为菱形,
为菱形,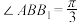 ,
,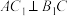 .
. .
.
(2)已知平面 平面
平面 ,求二面角
,求二面角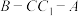 的正弦值.
的正弦值.
 中,
中, ,四边形
,四边形 为菱形,
为菱形,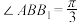 ,
,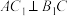 .
.
 .
.(2)已知平面
 平面
平面 ,求二面角
,求二面角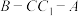 的正弦值.
的正弦值.
您最近一年使用:0次
7日内更新
|
941次组卷
|
4卷引用:河北省秦皇岛市青龙满族自治县第一中学2024届高三下学期5月模拟考试数学试题
3 . “完全数”是一类特殊的自然数,它的所有正因数的和等于它自身的两倍.寻找“完全数”需要用到函数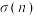 ,记函数
,记函数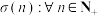 ,
,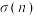 为
为 的所有正因数之和.
的所有正因数之和.
(1)判断28是否为完全数,并说明理由.
(2)已知 ,若
,若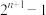 为质数,证明:
为质数,证明: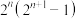 为完全数.
为完全数.
(3)已知 ,求
,求 ,
,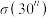 的值.
的值.
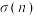 ,记函数
,记函数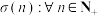 ,
,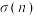 为
为 的所有正因数之和.
的所有正因数之和.(1)判断28是否为完全数,并说明理由.
(2)已知
 ,若
,若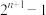 为质数,证明:
为质数,证明: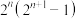 为完全数.
为完全数.(3)已知
 ,求
,求 ,
,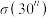 的值.
的值.
您最近一年使用:0次
7日内更新
|
386次组卷
|
3卷引用:河北省秦皇岛市青龙满族自治县第一中学2024届高三下学期5月模拟考试数学试题
名校
解题方法
4 . 教练统计了甲12次投篮训练的投篮次数和乙8次投篮训练的投篮次数,得到如下数据:
已知甲12次投篮次数的方差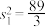 ,乙8次投篮次数的方差
,乙8次投篮次数的方差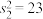 .
.
(1)求这20次投篮次数的平均数 与方差
与方差 .
.
(2)甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为 ,乙每次投篮的命中率均为
,乙每次投篮的命中率均为 .已知第一次投篮的人是甲,且甲、乙总共投篮了3次,
.已知第一次投篮的人是甲,且甲、乙总共投篮了3次, 表示甲投篮的次数,求
表示甲投篮的次数,求 的分布列与期望.
的分布列与期望.
甲 | 77 | 73 | 77 | 81 | 85 | 81 | 77 | 85 | 93 | 73 | 77 | 81 |
乙 | 71 | 81 | 73 | 73 | 71 | 73 | 85 | 73 |
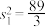 ,乙8次投篮次数的方差
,乙8次投篮次数的方差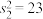 .
.(1)求这20次投篮次数的平均数
 与方差
与方差 .
.(2)甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为
 ,乙每次投篮的命中率均为
,乙每次投篮的命中率均为 .已知第一次投篮的人是甲,且甲、乙总共投篮了3次,
.已知第一次投篮的人是甲,且甲、乙总共投篮了3次, 表示甲投篮的次数,求
表示甲投篮的次数,求 的分布列与期望.
的分布列与期望.
您最近一年使用:0次
7日内更新
|
562次组卷
|
3卷引用:河北省秦皇岛市青龙满族自治县第一中学2024届高三下学期5月模拟考试数学试题
名校
5 . 已知函数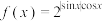 ,则( )
,则( )
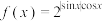 ,则( )
,则( )A. 是偶函数; 是偶函数; | B. 是周期为 是周期为 的周期函数; 的周期函数; |
C. 在 在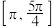 上单调递增; 上单调递增; | D. 的最小值为 的最小值为 . . |
您最近一年使用:0次
7日内更新
|
661次组卷
|
3卷引用:河北省秦皇岛市青龙满族自治县第一中学2024届高三下学期5月模拟考试数学试题
名校
解题方法
6 . 在 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且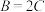 ,
, ,则( )
,则( )
 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且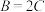 ,
, ,则( )
,则( )A. 为直角三角形 为直角三角形 | B. 为锐角三角形 为锐角三角形 |
C. 为钝角三角形 为钝角三角形 | D. 的形状无法确定 的形状无法确定 |
您最近一年使用:0次
7日内更新
|
757次组卷
|
3卷引用:河北省秦皇岛市青龙满族自治县第一中学2024届高三下学期5月模拟考试数学试题
名校
解题方法
7 . 假设在某种细菌培养过程中,正常细菌每小时分裂1次(1个正常细菌分裂成2个正常细菌和1个非正常细菌),非正常细菌每小时分裂1次(1个非正常细菌分裂成2个非正常细菌).若1个正常细菌经过14小时的培养,则可分裂成的细菌的个数为( )
A.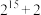 | B.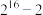 | C. | D.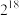 |
您最近一年使用:0次
7日内更新
|
528次组卷
|
4卷引用:河北省秦皇岛市青龙满族自治县第一中学2024届高三下学期5月模拟考试数学试题
名校
解题方法
8 . 在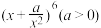 的展开式中,常数项为75,则
的展开式中,常数项为75,则
________ .
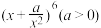 的展开式中,常数项为75,则
的展开式中,常数项为75,则
您最近一年使用:0次
7日内更新
|
260次组卷
|
2卷引用:河北省唐县第一中学2024届高三第三次模拟考试数学试题
名校
9 . 如图1,在等腰梯形 中,
中, ,
, ,
,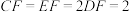 ,
,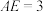 ,
,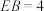 ,将四边形
,将四边形 沿
沿 进行折叠,使
进行折叠,使 到达
到达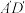 位置,且平面
位置,且平面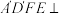 平面
平面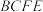 ,连接
,连接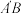 ,
,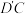 ,如图2,则( )
,如图2,则( )
 中,
中, ,
, ,
,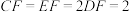 ,
,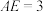 ,
,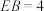 ,将四边形
,将四边形 沿
沿 进行折叠,使
进行折叠,使 到达
到达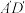 位置,且平面
位置,且平面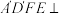 平面
平面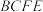 ,连接
,连接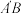 ,
,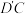 ,如图2,则( )
,如图2,则( )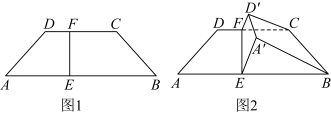
A. | B.平面 平面 平面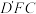 |
C.多面体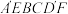 为三棱台 为三棱台 | D.直线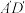 与平面 与平面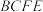 所成的角为 所成的角为 |
您最近一年使用:0次
2024-06-15更新
|
756次组卷
|
8卷引用:河北省保定市九校2024届高三下学期二模数学试题
河北省保定市九校2024届高三下学期二模数学试题山西省晋城市2024届高三第三次模拟考试数学试题浙江省强基联盟2024届高三下学期5月全国“优创名校”联考数学试题(已下线)第四套 艺体生新高考全真模拟 (三模重组卷)辽宁省抚顺市六校协作体2024届高三下学期5月模拟考试数学试卷(已下线)专题4 立体几何中的动态问题【讲】广西钦州市2024届高三年级第三次教学质量监测 数学(已下线)核心考点8 立体几何中综合问题 B提升卷 (高一期末考试必考的10大核心考点)
名校
解题方法
10 . 已知函数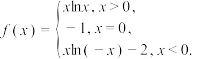 若关于
若关于 的方程
的方程 有5个不同的实数根,则
有5个不同的实数根,则 的取值范围是( )
的取值范围是( )
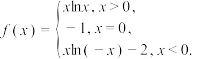 若关于
若关于 的方程
的方程 有5个不同的实数根,则
有5个不同的实数根,则 的取值范围是( )
的取值范围是( )A. | B. | C.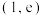 | D.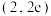 |
您最近一年使用:0次



