名校
1 . 已知函数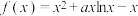
(1)当 时,求
时,求 的零点;
的零点;
(2)若 恰有两个极值点,求
恰有两个极值点,求 的取值范围.
的取值范围.
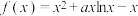
(1)当
 时,求
时,求 的零点;
的零点;(2)若
 恰有两个极值点,求
恰有两个极值点,求 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
455次组卷
|
4卷引用:吉林省吉林市第一中学等校2023-2024学年高二下学期5月期中联考数学试题
名校
解题方法
2 . 已知双曲线 的左、右顶点分别为
的左、右顶点分别为 ,
, ,渐近线方程为
,渐近线方程为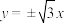 ,过左焦点
,过左焦点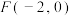 的直线
的直线 与
与 交于
交于 ,
, 两点.
两点.
(1)设直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,求
,求 的值;
的值;
(2)若直线 与直线
与直线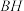 的交点为
的交点为 ,试问双曲线
,试问双曲线 上是否存在定点
上是否存在定点 ,使得
,使得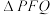 的面积为定值?若存在,求出定点
的面积为定值?若存在,求出定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 的左、右顶点分别为
的左、右顶点分别为 ,
, ,渐近线方程为
,渐近线方程为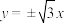 ,过左焦点
,过左焦点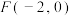 的直线
的直线 与
与 交于
交于 ,
, 两点.
两点.(1)设直线
 ,
, 的斜率分别为
的斜率分别为 ,
, ,求
,求 的值;
的值;(2)若直线
 与直线
与直线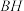 的交点为
的交点为 ,试问双曲线
,试问双曲线 上是否存在定点
上是否存在定点 ,使得
,使得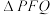 的面积为定值?若存在,求出定点
的面积为定值?若存在,求出定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近一年使用:0次
2024-06-14更新
|
381次组卷
|
3卷引用:吉林省长春市实验中学2023-2024学年高三下学期对位演练考试数学试卷(七)
名校
3 . 在信息理论中, 和
和 是两个取值相同的离散型随机变量,分布列分别为:
是两个取值相同的离散型随机变量,分布列分别为: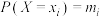 ,
, ,
,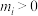 ,
, ,
,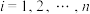 ,
,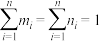 .定义随机变量
.定义随机变量 的信息量
的信息量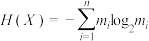 ,
, 和
和 的“距离”
的“距离”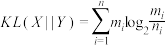 .
.
(1)若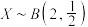 ,求
,求 ;
;
(2)已知发报台发出信号为0和1,接收台收到信号只有0和1.现发报台发出信号为0的概率为 ,由于通信信号受到干扰,发出信号0接收台收到信号为0的概率为
,由于通信信号受到干扰,发出信号0接收台收到信号为0的概率为 ,发出信号1接收台收到信号为1的概率为
,发出信号1接收台收到信号为1的概率为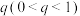 .
.
(ⅰ)若接收台收到信号为0,求发报台发出信号为0的概率;(用 ,
, 表示结果)
表示结果)
(ⅱ)记随机变量 和
和 分别为发出信号和收到信号,证明:
分别为发出信号和收到信号,证明: .
.
 和
和 是两个取值相同的离散型随机变量,分布列分别为:
是两个取值相同的离散型随机变量,分布列分别为: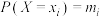 ,
, ,
,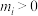 ,
, ,
,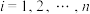 ,
,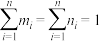 .定义随机变量
.定义随机变量 的信息量
的信息量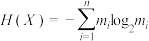 ,
, 和
和 的“距离”
的“距离”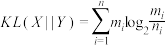 .
.(1)若
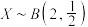 ,求
,求 ;
;(2)已知发报台发出信号为0和1,接收台收到信号只有0和1.现发报台发出信号为0的概率为
 ,由于通信信号受到干扰,发出信号0接收台收到信号为0的概率为
,由于通信信号受到干扰,发出信号0接收台收到信号为0的概率为 ,发出信号1接收台收到信号为1的概率为
,发出信号1接收台收到信号为1的概率为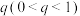 .
.(ⅰ)若接收台收到信号为0,求发报台发出信号为0的概率;(用
 ,
, 表示结果)
表示结果)(ⅱ)记随机变量
 和
和 分别为发出信号和收到信号,证明:
分别为发出信号和收到信号,证明: .
.
您最近一年使用:0次
2024-06-14更新
|
649次组卷
|
4卷引用:吉林省长春市实验中学2023-2024学年高三下学期对位演练考试数学试卷(七)
名校
解题方法
4 . 已知函数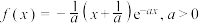 .
.
(1)若 的极小值为-4,求
的极小值为-4,求 的值;
的值;
(2)若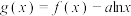 有两个不同的极值点
有两个不同的极值点 ,证明:
,证明: .
.
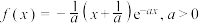 .
.(1)若
 的极小值为-4,求
的极小值为-4,求 的值;
的值;(2)若
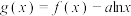 有两个不同的极值点
有两个不同的极值点 ,证明:
,证明: .
.
您最近一年使用:0次
5 . 函数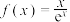 与
与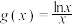 之间的关系非常密切,号称函数中的双子座,以下说法正确的是( )
之间的关系非常密切,号称函数中的双子座,以下说法正确的是( )
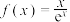 与
与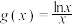 之间的关系非常密切,号称函数中的双子座,以下说法正确的是( )
之间的关系非常密切,号称函数中的双子座,以下说法正确的是( )A.若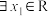 , ,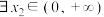 ,使得 ,使得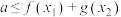 成立,则 成立,则 |
B.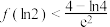 |
C.直线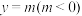 与两个函数图象交点的横坐标之积的范围是 与两个函数图象交点的横坐标之积的范围是 |
D.若直线 过两个函数图象的公共点,则直线 过两个函数图象的公共点,则直线 与两个函数图象的所有交点横坐标从小到大排列依次构成等比数列 与两个函数图象的所有交点横坐标从小到大排列依次构成等比数列 |
您最近一年使用:0次
6 . 对于数列 ,称
,称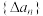 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 .对正整数
.对正整数 ,称
,称 为数列
为数列 的
的 阶差分数列,其中
阶差分数列,其中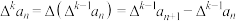 已知数列
已知数列 的首项
的首项 ,且
,且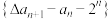 为
为 的二阶差分数列.
的二阶差分数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 为数列
为数列 的一阶差分数列,对
的一阶差分数列,对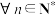 ,是否都有
,是否都有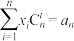 成立?并说明理由;(其中
成立?并说明理由;(其中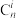 为组合数)
为组合数)
(3)对于(2)中的数列 ,令
,令 ,其中
,其中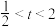 .证明:
.证明: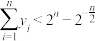 .
.
 ,称
,称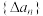 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 .对正整数
.对正整数 ,称
,称 为数列
为数列 的
的 阶差分数列,其中
阶差分数列,其中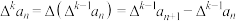 已知数列
已知数列 的首项
的首项 ,且
,且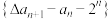 为
为 的二阶差分数列.
的二阶差分数列.(1)求数列
 的通项公式;
的通项公式;(2)设
 为数列
为数列 的一阶差分数列,对
的一阶差分数列,对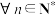 ,是否都有
,是否都有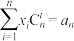 成立?并说明理由;(其中
成立?并说明理由;(其中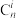 为组合数)
为组合数)(3)对于(2)中的数列
 ,令
,令 ,其中
,其中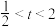 .证明:
.证明: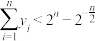 .
.
您最近一年使用:0次
2024-05-09更新
|
736次组卷
|
3卷引用:吉林省长春市东北师范大学附属中学2024届高三下学期第五次模拟考试数学试题
名校
7 . 已知函数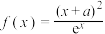 .
.
(1)讨论 的单调性;
的单调性;
(2)设 分别是
分别是 的极小值点和极大值点,记
的极小值点和极大值点,记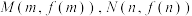 .
.
(i)证明:直线 与曲线
与曲线 交于除
交于除 外另一点
外另一点 ;
;
(ii)在(i)结论下,判断是否存在定值 且
且 ,使
,使 ,若存在,请求出
,若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
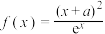 .
.(1)讨论
 的单调性;
的单调性;(2)设
 分别是
分别是 的极小值点和极大值点,记
的极小值点和极大值点,记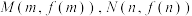 .
.(i)证明:直线
 与曲线
与曲线 交于除
交于除 外另一点
外另一点 ;
;(ii)在(i)结论下,判断是否存在定值
 且
且 ,使
,使 ,若存在,请求出
,若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2024-04-13更新
|
440次组卷
|
2卷引用:吉林省吉林地区普通高中2024届高三第三次模拟考试数学试题
8 . 如图,已知双曲线 的离心率为2,点
的离心率为2,点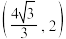 在
在 上,
上, 为双曲线的左、右顶点,
为双曲线的左、右顶点, 为
为 右支上的动点,直线
右支上的动点,直线 和直线
和直线 交于点
交于点 ,直线
,直线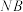 交
交 的右支于点
的右支于点 .
. 的方程;
的方程;
(2)探究直线 是否过定点,若过定点,求出该定点坐标;否则,请说明理由;
是否过定点,若过定点,求出该定点坐标;否则,请说明理由;
(3)设 分别为
分别为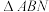 和
和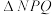 的外接圆面积,求
的外接圆面积,求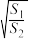 的取值范围.
的取值范围.
 的离心率为2,点
的离心率为2,点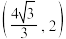 在
在 上,
上, 为双曲线的左、右顶点,
为双曲线的左、右顶点, 为
为 右支上的动点,直线
右支上的动点,直线 和直线
和直线 交于点
交于点 ,直线
,直线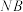 交
交 的右支于点
的右支于点 .
.
 的方程;
的方程;(2)探究直线
 是否过定点,若过定点,求出该定点坐标;否则,请说明理由;
是否过定点,若过定点,求出该定点坐标;否则,请说明理由;(3)设
 分别为
分别为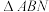 和
和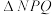 的外接圆面积,求
的外接圆面积,求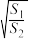 的取值范围.
的取值范围.
您最近一年使用:0次
2024-04-10更新
|
757次组卷
|
3卷引用:吉林市第一中学2024届高三高考适应性训练(二)数学试题
9 . 与大家熟悉的黄金分割相类似的还有一个白银分割,比如A4纸中就包含着白银分割率.若一个数列从0和1开始,以后每一个数都是前面的数的两倍加上再前面的数:0,1,2,5,12,29,70,169,408,985,2378,…,则随着n趋于无穷大,其前一项与后一项的比值越来越接近白银分割率.记该数列为 ,其前n项和为
,其前n项和为 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.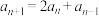 ( ( ) ) | B.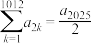 |
C.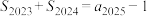 | D.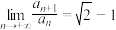 |
您最近一年使用:0次
解题方法
10 . 已知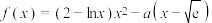 有两个极值点
有两个极值点 .
.
(1)求实数a的取值范围;
(2)证明:
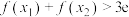 .
.
您最近一年使用:0次



