江苏省宿迁市2023-2024学年高二上学期期末调研测试数学试卷
江苏
高二
期末
2024-03-02
434次
整体难度:
适中
考查范围:
平面解析几何、数列、集合与常用逻辑用语、函数与导数、新文化试题分类、等式与不等式
一、单选题 添加题型下试题
 的离心率为
的离心率为 ,则椭圆的长轴长为( )
,则椭圆的长轴长为( )A.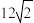 | B. | C. | D.6 |
【知识点】 求椭圆的长轴、短轴 根据离心率求椭圆的标准方程
 满足
满足 ,
, ,则
,则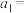 ( )
( )A. | B. | C. | D. |
【知识点】 等比数列通项公式的基本量计算
 ”是“方程
”是“方程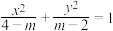 表示双曲线”的( )
表示双曲线”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
【知识点】 判断命题的充分不必要条件 根据方程表示双曲线求参数的范围
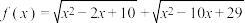 取得最小值时,实数
取得最小值时,实数 的值为( )
的值为( )A.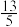 | B.3 | C.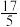 | D.4 |
【知识点】 求平面两点间的距离 用两点间的距离公式求函数最值
 是定义在
是定义在 上的奇函数,对任意实数
上的奇函数,对任意实数 恒有
恒有 ,则( )
,则( )A. | B.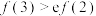 |
C.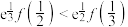 | D.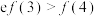 |
【知识点】 用导数判断或证明已知函数的单调性 比较函数值的大小关系
二、多选题 添加题型下试题
 的前
的前 项和
项和 ,则下列说法正确的是( )
,则下列说法正确的是( )A.数列 为递减数列 为递减数列 |
B.数列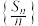 为等差数列 为等差数列 |
C.若数列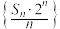 为递减数列,则 为递减数列,则 |
D.当 时,则 时,则 取最大值时 取最大值时 |
 :
: (
( )的焦点为
)的焦点为 ,过拋物线
,过拋物线 上一点
上一点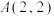 作两条斜率之和为0的直线,与
作两条斜率之和为0的直线,与 的另外两个交点分别为
的另外两个交点分别为 ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )A. 的准线方程是 的准线方程是 |
B.直线 的斜率为定值 的斜率为定值 |
C.若圆 与以 与以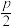 为半径的圆 为半径的圆 相外切,则圆 相外切,则圆 与直线 与直线 相切 相切 |
D.若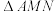 的面积为 的面积为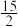 ,则直线 ,则直线 的方程为 的方程为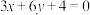 |
 :
: ,过圆
,过圆 外一点
外一点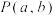 作圆
作圆 的切线,切点为
的切线,切点为 ,
, ,直线
,直线 与直线
与直线 相交于点
相交于点 ,则下列说法正确的是( )
,则下列说法正确的是( )A.若点 在直线 在直线 上,则直线 上,则直线 过定点 过定点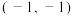 |
B.当 取得最小值时,点 取得最小值时,点 在圆 在圆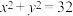 上 上 |
C.直线 , , 关于直线 关于直线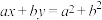 对称 对称 |
D.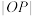 与 与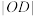 的乘积为定值4 的乘积为定值4 |
三、填空题 添加题型下试题
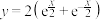 的单调增区间为
的单调增区间为【知识点】 利用导数求函数的单调区间(不含参)
 ,
, 的距离之比为定值
的距离之比为定值 (
( 且
且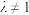 )的点所形成的图形是圆,后来,人们把这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知点
)的点所形成的图形是圆,后来,人们把这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知点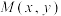 到两个定点
到两个定点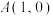 ,
, 的距离之比为2,则
的距离之比为2,则 的取值范围为
的取值范围为【知识点】 轨迹问题——圆 由直线与圆的位置关系求参数 平面解析几何
四、解答题 添加题型下试题
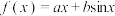 的图象在点
的图象在点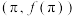 处的切线方程是
处的切线方程是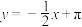 .
.(1)求
 ,
, 的值;
的值;(2)求函数
 在区间
在区间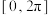 上的最大值与最小值.
上的最大值与最小值.
【知识点】 已知切线(斜率)求参数 由导数求函数的最值(不含参)
 满足:
满足: ,且对任意的
,且对任意的 ,都有
,都有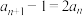 .
.(1)求数列
 的通项公式;
的通项公式;(2)求数列
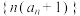 的前
的前 项和
项和 .
.
【知识点】 由递推关系式求通项公式 写出等比数列的通项公式 错位相减法求和
 和
和 互相垂直,墙角内有一景观
互相垂直,墙角内有一景观 ,
, 到墙角线
到墙角线 、
、 的距离分别为20米、10米,学校欲过景观
的距离分别为20米、10米,学校欲过景观 修建一条直线型走廊
修建一条直线型走廊 ,其中
,其中 的两个端点分别在这两墙角线上.
的两个端点分别在这两墙角线上.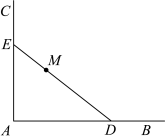
 的面积最小,应如何设计直线型走廊
的面积最小,应如何设计直线型走廊 ?
?(2)考虑到修建直线型走廊
 的成本,怎样设计,才能使走廊
的成本,怎样设计,才能使走廊 的长度最短?
的长度最短?
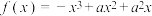 ,
,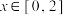 .
.(1)当
 时,求
时,求 的值域;
的值域;(2)若对任意
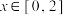 ,不等式
,不等式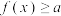 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【知识点】 由导数求函数的最值(不含参) 利用导数研究不等式恒成立问题
 :
: (
( ,
, )的左、右顶点分别为
)的左、右顶点分别为 ,
, ,右焦点
,右焦点 到渐近线的距离为1,且离心率为
到渐近线的距离为1,且离心率为 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)过点
 的直线
的直线 (直线
(直线 的斜率不为0)与双曲线
的斜率不为0)与双曲线 交于
交于 ,
, 两点,若
两点,若 ,
, 分别为直线
分别为直线 ,
, 与
与 轴的交点,记
轴的交点,记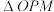 ,
,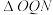 的面积分别记为
的面积分别记为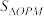 ,
,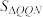 ,求
,求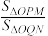 的值.
的值.
试卷分析
导出试卷题型(共 19题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.85 | 直线的倾斜角 已知两点求斜率 | |
| 2 | 0.85 | 求椭圆的长轴、短轴 根据离心率求椭圆的标准方程 | |
| 3 | 0.85 | 等比数列通项公式的基本量计算 | |
| 4 | 0.85 | 判断命题的充分不必要条件 根据方程表示双曲线求参数的范围 | |
| 5 | 0.85 | 求平面两点间的距离 用两点间的距离公式求函数最值 | |
| 6 | 0.65 | 椭圆定义及辨析 双曲线定义的理解 | |
| 7 | 0.65 | 点与圆的位置关系求参数 由直线与圆的位置关系求参数 | |
| 8 | 0.65 | 用导数判断或证明已知函数的单调性 比较函数值的大小关系 | |
| 二、多选题 | |||
| 9 | 0.65 | 由递推关系证明数列是等差数列 求等差数列前n项和的最值 利用an与sn关系求通项或项 根据数列的单调性求参数 | |
| 10 | 0.65 | 抛物线定义的理解 根据抛物线方程求焦点或准线 根据抛物线上的点求标准方程 抛物线中的三角形或四边形面积问题 | |
| 11 | 0.4 | 直线过定点问题 直线关于直线对称问题 由直线与圆的位置关系求参数 切点弦及其方程 | |
| 三、填空题 | |||
| 12 | 0.65 | 利用导数求函数的单调区间(不含参) | 单空题 |
| 13 | 0.65 | 轨迹问题——圆 由直线与圆的位置关系求参数 平面解析几何 | 单空题 |
| 14 | 0.65 | 利用an与sn关系求通项或项 构造法求数列通项 | 单空题 |
| 四、解答题 | |||
| 15 | 0.65 | 已知切线(斜率)求参数 由导数求函数的最值(不含参) | 问答题 |
| 16 | 0.65 | 由递推关系式求通项公式 写出等比数列的通项公式 错位相减法求和 | 问答题 |
| 17 | 0.65 | 由导数求函数的最值(不含参) 基本(均值)不等式的应用 基本不等式求和的最小值 | 应用题 |
| 18 | 0.65 | 由导数求函数的最值(不含参) 利用导数研究不等式恒成立问题 | 问答题 |
| 19 | 0.65 | 根据离心率求双曲线的标准方程 求双曲线中三角形(四边形)的面积问题 双曲线中的定值问题 根据韦达定理求参数 | 问答题 |

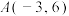 ,
,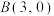 ,则直线
,则直线


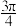
 与双曲线
与双曲线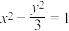 有相同的焦点
有相同的焦点 ,
, ,且椭圆与双曲线在第一象限的交点为
,且椭圆与双曲线在第一象限的交点为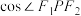 的值为(
的值为(



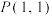 在圆
在圆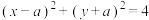 的外部,若圆
的外部,若圆 ,则正数
,则正数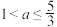
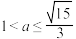
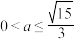

 ,
,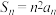 (
(

