18. “2021年全国城市节约用水宣传周”已于5月9日至15日举行,某市围绕“贯彻新发展理念,建设节水型城市”这一主题,开展了形式式样、内容丰富的活动,进一步增强全民保护水资源、防治水污染、节约用水的意识,为了解活动开展成效,该市的某街道办事处工作人员赴一小区调查住户的节约用水情况,随机抽取了300名业主进行节约用水调查评分,将得到的分数分成6组:[70,75],(75,80],(80,85],(85,90],(90,95],(95,100],得到如图所示的频率分布直方图.
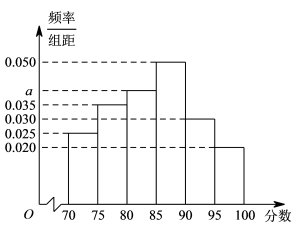
(1)求

的值,并求这300名业主评分的中位数;
(2)若先用分层抽样的方法从评分在(90,95]和(95,100]的业主中抽取5人,然后再从抽出的这5名业主中任意选取2人作进一步访谈,求这2人中至少有1人的评分在(95,100]的概率.