17. 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段
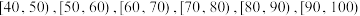
进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如下):

(Ⅰ)体育成绩大于或等于70分的学生常被称为“体育良好”.已知该校高一年级有1000名学生,试估计高一全年级中“体育良好”的学生人数;
(Ⅱ)为分析学生平时的体育活动情况,现从体育成绩在
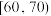
和
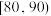
的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在
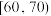
的概率;
(Ⅲ)假设甲、乙、丙三人的体育成绩分别为

且分别在
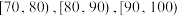
三组中,其中
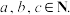
当数据

的方差

最小时,写出

的值.(结论不要求证明)
(注: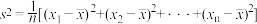 ,其中
,其中 为数据
为数据 的平均数)
的平均数)