1 . 如图正方体 的棱长为2,
的棱长为2, 平面
平面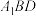 ;
;
(2)证明: 平面
平面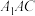 ;
;
(3)求三棱锥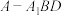 的体积;
的体积;
(4)二面角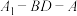 的正弦值.
的正弦值.
 的棱长为2,
的棱长为2,
 平面
平面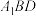 ;
;(2)证明:
 平面
平面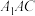 ;
;(3)求三棱锥
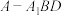 的体积;
的体积;(4)二面角
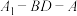 的正弦值.
的正弦值.
您最近一年使用:0次
名校
解题方法
2 . 已知数列 满足
满足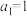 ,
, ,则
,则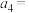 ( )
( )
 满足
满足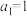 ,
, ,则
,则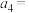 ( )
( )A. | B.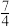 | C. | D. |
您最近一年使用:0次
名校
3 . 已知函数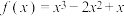 .
.
(1)求函数 的图象在点
的图象在点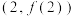 处的切线方程;
处的切线方程;
(2)求函数 在区间
在区间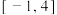 上的最大值与最小值.
上的最大值与最小值.
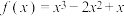 .
.(1)求函数
 的图象在点
的图象在点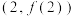 处的切线方程;
处的切线方程;(2)求函数
 在区间
在区间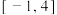 上的最大值与最小值.
上的最大值与最小值.
您最近一年使用:0次
4 . 已知数列 具有性质
具有性质 :
: 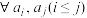 , 都
, 都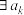 ,使得
,使得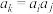 .
.
(1)分别判断以下两个数列是否满足性质 ,并说明理由;
,并说明理由;
(ⅰ)有穷数列 :
: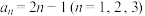 ;
;
(ⅱ)无穷数列 :
: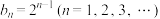 ;
;
(2)若有穷数列 满足性质
满足性质 ,且各项互不相等,求项数
,且各项互不相等,求项数 的最大值.
的最大值.
 具有性质
具有性质 :
: 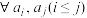 , 都
, 都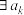 ,使得
,使得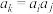 .
.(1)分别判断以下两个数列是否满足性质
 ,并说明理由;
,并说明理由;(ⅰ)有穷数列
 :
: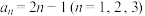 ;
;(ⅱ)无穷数列
 :
: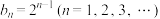 ;
;(2)若有穷数列
 满足性质
满足性质 ,且各项互不相等,求项数
,且各项互不相等,求项数 的最大值.
的最大值.
您最近一年使用:0次
5 . 求下列函数的导数.
(1)①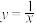 ;②
;② ;③
;③ ;
;
(2)① ;②
;②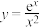 ;
;
(3)①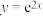 ;②
;②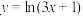 ;③
;③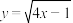 .
.
(1)①
 ;②
;② ;③
;③ ;
;(2)①
 ;②
;②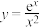 ;
;(3)①
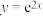 ;②
;②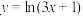 ;③
;③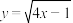 .
.
您最近一年使用:0次
6 . 如果函数 在区间
在区间 上连续,在区间
上连续,在区间 内可导,则“
内可导,则“ ”是“
”是“ 在
在 上单调递增”的( )
上单调递增”的( )
 在区间
在区间 上连续,在区间
上连续,在区间 内可导,则“
内可导,则“ ”是“
”是“ 在
在 上单调递增”的( )
上单调递增”的( )| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
7 . 求满足下列条件的直线 的方程.
的方程.
(1) 为曲线
为曲线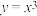 在
在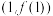 处的切线;
处的切线;
(2) 的斜率为
的斜率为 且与曲线
且与曲线 相切;
相切;
(3) 过原点且与曲线
过原点且与曲线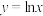 相切.
相切.
 的方程.
的方程.(1)
 为曲线
为曲线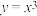 在
在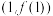 处的切线;
处的切线;(2)
 的斜率为
的斜率为 且与曲线
且与曲线 相切;
相切;(3)
 过原点且与曲线
过原点且与曲线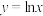 相切.
相切.
您最近一年使用:0次
8 . 已知函数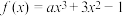 ,若
,若 存在唯一的零点
存在唯一的零点 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( )
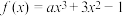 ,若
,若 存在唯一的零点
存在唯一的零点 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( )A. | B.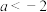 |
C.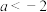 或 或 | D. |
您最近一年使用:0次
解题方法
9 . 已知锐角  中,
中, ,
, ,
,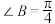 .
.
(1)求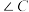 及
及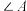 的值;
的值;
(2)求 及
及 面积.
面积.
 中,
中, ,
, ,
,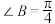 .
.(1)求
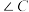 及
及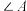 的值;
的值;(2)求
 及
及 面积.
面积.
您最近一年使用:0次
10 . 函数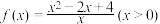 的最小值及取得最小值时
的最小值及取得最小值时 的值为( )
的值为( )
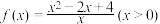 的最小值及取得最小值时
的最小值及取得最小值时 的值为( )
的值为( )A.当 时最小值为 时最小值为 | B.当 时最小值为 时最小值为 |
C.当 时最小值为 时最小值为 | D.当 时最小值为 时最小值为 |
您最近一年使用:0次



