1 . 下列结论中是正确的有( )
A.函数 的零点是 的零点是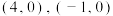 |
B.已知幂函数 的图象不过原点,则实数 的图象不过原点,则实数 的取值为1 的取值为1 |
C.函数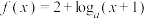 (其中 (其中 且 且 )的图象过定点 )的图象过定点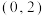 |
D.若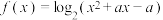 的值域为 的值域为 ,则实数 ,则实数 的取值范围是 的取值范围是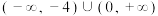 |
您最近一年使用:0次
2 . 如图,已知两质点A,B同时从点P出发,绕单位圆逆时针做匀速圆周运动,质点A,B运动的角速度分别为3rad/s和5rad/s,设两质点运动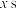 时这两质点间的距离为
时这两质点间的距离为 .
.
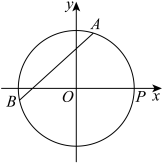
(1)求 的解析式;
的解析式;
(2)求这两质点从点P出发后第n次相遇的时间 (单位:s).
(单位:s).
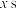 时这两质点间的距离为
时这两质点间的距离为 .
.
(1)求
 的解析式;
的解析式;(2)求这两质点从点P出发后第n次相遇的时间
 (单位:s).
(单位:s).
您最近一年使用:0次
2023-09-30更新
|
241次组卷
|
3卷引用:河南省2023-2024学年高三上学期一轮复习阶段性检测(三)数学试题
河南省2023-2024学年高三上学期一轮复习阶段性检测(三)数学试题江西省部分高中学校2024届高三上学期9月大联考数学试题(已下线)专题05 三角函数(5大易错点分析+解题模板+举一反三+易错题通关)
3 . 已知定义域为 的函数
的函数 满足
满足 ,且曲线
,且曲线 与曲线
与曲线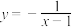 有且只有两个交点,则函数
有且只有两个交点,则函数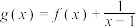 的零点之和是( )
的零点之和是( )
 的函数
的函数 满足
满足 ,且曲线
,且曲线 与曲线
与曲线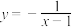 有且只有两个交点,则函数
有且只有两个交点,则函数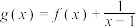 的零点之和是( )
的零点之和是( )| A.2 | B.-2 | C.4 | D.-4 |
您最近一年使用:0次
2023-09-28更新
|
620次组卷
|
5卷引用:河南省2023-2024学年高三上学期一轮复习阶段性检测(三)数学试题
河南省2023-2024学年高三上学期一轮复习阶段性检测(三)数学试题河北省邢台市五岳联盟2024届高三上学期9月月考数学试题江西省部分高中学校2024届高三上学期9月大联考数学试题(已下线)第四章:指数函数与对数函数章末重点题型复习(2)-【题型分类归纳】(人教A版2019必修第一册)【课后练】 第4.4节综合训练 课后作业-湘教版(2019)必修(第一册)第4章 幂函数、指数函数和对数函数
名校
解题方法
4 . 设 ,函数
,函数 ,
,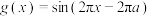 .
.
(1)若函数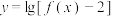 的值域是
的值域是 ,求
,求 的取值范围;
的取值范围;
(2)当 时,记函数
时,记函数 ,讨论
,讨论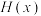 在区间
在区间 内零点的个数.
内零点的个数.
 ,函数
,函数 ,
,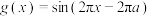 .
.(1)若函数
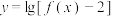 的值域是
的值域是 ,求
,求 的取值范围;
的取值范围;(2)当
 时,记函数
时,记函数 ,讨论
,讨论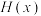 在区间
在区间 内零点的个数.
内零点的个数.
您最近一年使用:0次
2023-09-25更新
|
489次组卷
|
2卷引用:河南省周口市河南省基础教育教学研究院(普通合伙)等2校2022-2023学年高一上学期期末数学试题
名校
解题方法
5 . 设函数 的定义域为
的定义域为 ,若存在
,若存在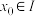 ,使得
,使得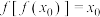 ,则称
,则称 是函数
是函数 的二阶不动点.下列各函数中,有且仅有一个二阶不动点的函数是( )
的二阶不动点.下列各函数中,有且仅有一个二阶不动点的函数是( )
 的定义域为
的定义域为 ,若存在
,若存在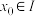 ,使得
,使得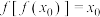 ,则称
,则称 是函数
是函数 的二阶不动点.下列各函数中,有且仅有一个二阶不动点的函数是( )
的二阶不动点.下列各函数中,有且仅有一个二阶不动点的函数是( )A.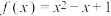 | B.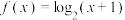 |
C.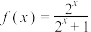 | D. |
您最近一年使用:0次
2023-09-25更新
|
1474次组卷
|
6卷引用:河南省周口市河南省基础教育教学研究院(普通合伙)等2校2022-2023学年高一上学期期末数学试题
河南省周口市河南省基础教育教学研究院(普通合伙)等2校2022-2023学年高一上学期期末数学试题(已下线)模块六 专题5 全真拔高模拟1 期末研习室高一人教A浙江省温州市鹿城区温州人文高级中学2023-2024学年高一上学期12月月考数学试题广东省2024届高三数学新改革适应性训练二(九省联考题型)(已下线)专题6 函数的零点问题(过关集训)(压轴题大全)(已下线)专题7 嵌套函数与函数迭代问题(过关集训)(压轴题大全)
6 . 已知函数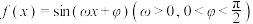 相邻两条对称轴距离为3,且
相邻两条对称轴距离为3,且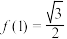 ,函数
,函数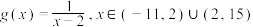 ,则方程
,则方程 的所有实根之和为
的所有实根之和为___________ .
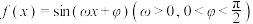 相邻两条对称轴距离为3,且
相邻两条对称轴距离为3,且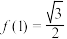 ,函数
,函数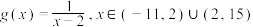 ,则方程
,则方程 的所有实根之和为
的所有实根之和为
您最近一年使用:0次
2023-09-14更新
|
389次组卷
|
2卷引用:河南省郑州外国语学校2023-2024学年高三上学期第三次调研考试数学试题
名校
解题方法
7 . 已知函数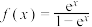 ,则( )
,则( )
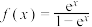 ,则( )
,则( )A. 在定义域上单调递增 在定义域上单调递增 |
B. 没有零点 没有零点 |
C.不存在平行于x轴且与曲线 相切的直线 相切的直线 |
D. 的图象是中心对称图形 的图象是中心对称图形 |
您最近一年使用:0次
2023-09-10更新
|
370次组卷
|
2卷引用:河南省天一联考2023-2024学年高三上学期调研考试数学试题
名校
8 . 已知函数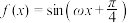
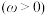 在区间
在区间 上有且仅有4条对称轴,给出下列四个结论:①
上有且仅有4条对称轴,给出下列四个结论:① 在区间
在区间 上有且仅有3个不同的零点;②
上有且仅有3个不同的零点;② 的最小正周期可能是
的最小正周期可能是 ;③
;③ 的取值范围是
的取值范围是 ;④
;④ 在区间
在区间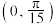 上单调递增.其中所有正确结论的序号是( )
上单调递增.其中所有正确结论的序号是( )
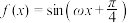
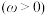 在区间
在区间 上有且仅有4条对称轴,给出下列四个结论:①
上有且仅有4条对称轴,给出下列四个结论:① 在区间
在区间 上有且仅有3个不同的零点;②
上有且仅有3个不同的零点;② 的最小正周期可能是
的最小正周期可能是 ;③
;③ 的取值范围是
的取值范围是 ;④
;④ 在区间
在区间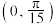 上单调递增.其中所有正确结论的序号是( )
上单调递增.其中所有正确结论的序号是( )| A.①④ | B.②③ | C.② | D.②③④ |
您最近一年使用:0次
2023-09-07更新
|
295次组卷
|
3卷引用:河南省三门峡市五县市2023-2024学年高一上学期1期末调研考试数学试题
解题方法
9 . 下列命题正确的是( )
A.若集合 有 有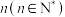 个元素,则 个元素,则 的真子集的个数为 的真子集的个数为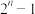 |
B.“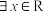 ,使 ,使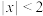 ”的否定是“ ”的否定是“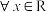 ,恒有 ,恒有 ” ” |
C.函数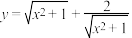 的最小值为 的最小值为 |
D.函数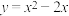 的零点为 的零点为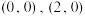 |
您最近一年使用:0次
名校
解题方法
10 . 已知函数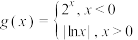 (
( 为自然对数的底数),则函数
为自然对数的底数),则函数 的零点个数为( )
的零点个数为( )
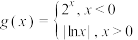 (
( 为自然对数的底数),则函数
为自然对数的底数),则函数 的零点个数为( )
的零点个数为( )| A.1 | B.3 | C.5 | D.7 |
您最近一年使用:0次
2023-08-31更新
|
2053次组卷
|
7卷引用:河南省2024届高三上学期起点考试数学试题
河南省2024届高三上学期起点考试数学试题河南省洛阳市洛宁县第一高级中学2023-2024学年高三上学期第二次月考数学试题(已下线)第四章 导数与函数的零点 专题三 复合函数零点问题 微点1 复合函数零点问题(一)(已下线)模块二 大招18 复合方程的实数根问题(已下线)2.10 函数与方程(高三一轮)【同步课时】提升卷(已下线)专题03 函数零点的综合应用六大类型-【常考压轴题】(苏教版2019必修第一册)(已下线)【必夺分】突破点13 函数的零点与方程的解



