名校
解题方法
1 . 如图,在长方形 中,
中,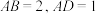 ,点
,点 在线段
在线段 (端点除外)上,现将
(端点除外)上,现将 沿
沿 折起为
折起为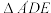 ,设
,设 ,二面角
,二面角 的大小为
的大小为 .若
.若 ,则三棱锥
,则三棱锥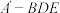 体积的最大值为
体积的最大值为______ .
 中,
中,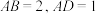 ,点
,点 在线段
在线段 (端点除外)上,现将
(端点除外)上,现将 沿
沿 折起为
折起为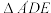 ,设
,设 ,二面角
,二面角 的大小为
的大小为 .若
.若 ,则三棱锥
,则三棱锥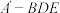 体积的最大值为
体积的最大值为
您最近一年使用:0次
名校
解题方法
2 . 下列物体,能够被整体放入长、宽、高分别为2,1,1(单位:m)的长方体容器(容器壁厚度忽略不计)内的有( )
| A.半径为0.6m的球体 |
| B.一组相对棱为1.4m,其余棱都为2m的四面体 |
| C.底面半径为0.005m,高为2.5m的圆柱体 |
| D.底面半径为0.6m,高为0.005m的圆柱体 |
您最近一年使用:0次
名校
解题方法
3 . 已知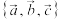 是空间的一个基底,
是空间的一个基底,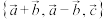 是空间的另一个基底,一向量
是空间的另一个基底,一向量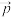 在基底
在基底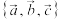 下的坐标为
下的坐标为 ,则向量
,则向量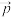 在基底
在基底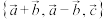 下的坐标是( )
下的坐标是( )
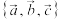 是空间的一个基底,
是空间的一个基底,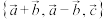 是空间的另一个基底,一向量
是空间的另一个基底,一向量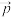 在基底
在基底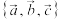 下的坐标为
下的坐标为 ,则向量
,则向量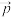 在基底
在基底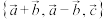 下的坐标是( )
下的坐标是( )A. | B.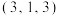 | C.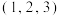 | D.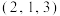 |
您最近一年使用:0次
2024-05-02更新
|
661次组卷
|
34卷引用:江西省临川第一中学2018-2019学年高二上学期期末考试数学(理)试题
江西省临川第一中学2018-2019学年高二上学期期末考试数学(理)试题(已下线)2019年12月12日《每日一题》选修2-1理数-空间向量的正交分解及其坐标表示人教A版(2019) 选择性必修第一册 必杀技 第一章 空间向量与立体几何 1.3 空间向量及其运算的坐标表示 1.3.1 空间直角坐标系 1.3.2 空间向量运算的坐标表示人教B版(2019) 选择性必修第一册 必杀技 第一章 空间向量与立体几何 1.1 空间向量及其运算 1.1.3 空间向量的坐标与空间直角坐标系 课时1 空间向量的坐标表示及其运算(已下线)考点33 空间角、空间向量及其应用-备战2022年高考数学一轮复习考点帮(浙江专用)北师大版(2019) 选修第一册 必杀技 第三章 3.2 空间向量运算的坐标表示及应用北师大版(2019) 选修第一册 突围者 第三章 第三节 课时1 空间向量基本定理重庆市万州第二高级中学2021-2022学年高二上学期第一次月考数学试题广东省梅州市大埔县田家炳实验中学2021-2022学年高二上学期第一次段考(10月)数学试题苏教版(2019) 选修第二册 名师精选 第六章 第一单元 空间向量及其运算、空间向量的坐标表示 A卷(已下线)专题1.6 空间向量与立体几何(能力提升卷)空间向量及其运算的坐标表示(已下线)专题32 空间向量及其应用-1(已下线)1.1.3 空间向量的坐标与空间直角坐标系河南省中原名校2022-2023学年高二上学期第二次联考数学试题河南省郑州市第一〇六高级中学2022-2023学年高二上学期9月月考数学试题山东省潍坊市寿光市第一中学2021-2022学年高二上学期期末数学试题山东省淄博市淄博第五中学2022-2023学年高二上学期期末数学试题安徽省宿州市萧县鹏程中学2021-2022学年高一远志班下学期第一次质量检测数学试题3.3 空间向量基本定理及空间向量运算的坐标表示——2022-2023学年高二数学北师大版(2019)选择性必修第一册(已下线)第3讲 空间向量及其运算的坐标表示 (1)第一章 空间向量与立体几何 讲核心01甘肃省庆阳第二中学2022-2023学年高二下学期第一次月考数学试题(已下线)第06讲 空间向量及其运算的坐标表示 (1)(已下线)第一章:空间向量与立体几何章末综合检测卷-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)(已下线)第04讲 1.3 空间向量及其运算的坐标表示(2)(已下线)第05讲 空间向量及其应用(十六大题型)(讲义)-1(已下线)专题 1.1 空间向量基本定理及基底求最值12种题型(1)辽宁省沈阳市新民市第一高级中学2023-2024学年高二下学期期初考试数学试题江苏省连云港市厉庄高级中学2023-2024学年高二下学期期中数学检测试题(已下线)专题01 空间向量表示及运算--高二期末考点大串讲(苏教版2019选择性必修第二册)(已下线)第03讲 空间向量基本定理-【暑假预科讲义】(人教A版2019选择性必修第一册)(已下线)第03讲 空间向量基本定理-【暑假自学课】(人教A版2019选择性必修第一册)(已下线)1.2空间向量基本定理——随堂检测
4 . 在三棱锥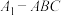 中,
中,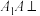 平面
平面 ,
,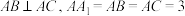 ,P为
,P为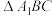 内的一个动点(包括边界),
内的一个动点(包括边界), 与平面
与平面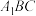 所成的角为
所成的角为 ,则( )
,则( )
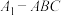 中,
中,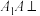 平面
平面 ,
,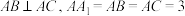 ,P为
,P为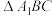 内的一个动点(包括边界),
内的一个动点(包括边界), 与平面
与平面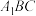 所成的角为
所成的角为 ,则( )
,则( )A.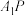 的最小值为 的最小值为 | B.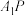 的最大值为 的最大值为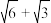 |
C.有且仅有一个点P,使得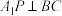 | D.所有满足条件的线段 形成的曲面面积 形成的曲面面积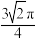 |
您最近一年使用:0次
2024-04-15更新
|
408次组卷
|
8卷引用:河北省金科大联考2024届高三上学期12月月考数学试题
5 . 如图,已知正方体 的棱长为
的棱长为 ,点
,点 为
为 的中点,点
的中点,点 为正方形
为正方形 内
内 包含边界
包含边界 的动点,则( )
的动点,则( )
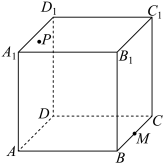
 的棱长为
的棱长为 ,点
,点 为
为 的中点,点
的中点,点 为正方形
为正方形 内
内 包含边界
包含边界 的动点,则( )
的动点,则( )
A.满足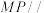 平面 平面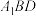 的点 的点 的轨迹为线段 的轨迹为线段 |
B.若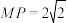 ,则动点 ,则动点 的轨迹长度为 的轨迹长度为 |
C.直线 与直线 与直线 所成角的范围为 所成角的范围为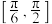 |
D.满足 的点 的点 的轨迹长度为 的轨迹长度为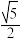 |
您最近一年使用:0次
2024-03-29更新
|
1062次组卷
|
5卷引用:山东省菏泽第一中学南京路校区2024届高三下学期3月月考数学试题
山东省菏泽第一中学南京路校区2024届高三下学期3月月考数学试题湖南省岳阳市2024届高三下学期教学质量监测(二)数学试题(已下线)专题3 立体几何中的范围、最值问题【讲】(已下线)专题4 立体几何中的动态问题【练】(已下线)6.1 空间几何的体积与表面积
6 . 直三棱柱 中,
中,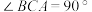 ,点
,点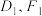 分别是
分别是 的中点,若
的中点,若 ,求
,求 与
与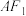 间的距离.
间的距离.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
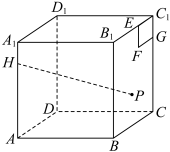
7 . 如图,已知正方体 的棱长为4,点
的棱长为4,点 在棱
在棱 上,且
上,且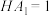 ,在侧面
,在侧面 内作边长为1的正方形
内作边长为1的正方形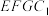 ,
, 是侧面
是侧面 内的动点,且点
内的动点,且点 到平面
到平面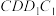 的距离等于线段
的距离等于线段 的长.当点
的长.当点 运动时,
运动时, 的最小值是
的最小值是
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
8 . 如图, 为圆锥的顶点,该圆锥的母线长为
为圆锥的顶点,该圆锥的母线长为 米,底面圆的半径为
米,底面圆的半径为 米,
米, 为底面圆周上一点,一只蚂蚁从点
为底面圆周上一点,一只蚂蚁从点 出发沿圆锥的侧面爬行一周到达母线
出发沿圆锥的侧面爬行一周到达母线 上的一点
上的一点 ,则( )
,则( )
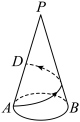
 为圆锥的顶点,该圆锥的母线长为
为圆锥的顶点,该圆锥的母线长为 米,底面圆的半径为
米,底面圆的半径为 米,
米, 为底面圆周上一点,一只蚂蚁从点
为底面圆周上一点,一只蚂蚁从点 出发沿圆锥的侧面爬行一周到达母线
出发沿圆锥的侧面爬行一周到达母线 上的一点
上的一点 ,则( )
,则( )
A.蚂蚁爬行的最短路程为 米 米 |
B.当蚂蚁爬行的路程最短时,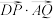 的最大值为 的最大值为 |
C.蚂蚁爬行的最短路程为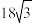 米 米 |
D.当蚂蚁爬行的路程最短时,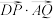 的最大值为 的最大值为 |
您最近一年使用:0次
名校
解题方法
9 . 三阶行列式是解决复杂代数运算的算法,其运算法则如下: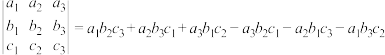
 若
若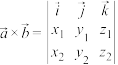 ,则称
,则称 为空间向量
为空间向量 与
与 的叉乘,其中
的叉乘,其中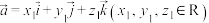 ,
,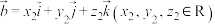 ,
, 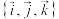 为单位正交基底. 以
为单位正交基底. 以  为坐标原点、分别以
为坐标原点、分别以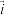 ,
, ,
,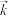 的方向为
的方向为  轴、
轴、  轴、
轴、  轴的正方向建立空间直角坐标系,已知
轴的正方向建立空间直角坐标系,已知 ,
, 是空间直角坐标系中异于
是空间直角坐标系中异于  的不同两点
的不同两点
(1)①若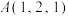 ,
, ,求
,求 ;
;
②证明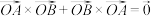 .
.
(2)记 的面积为
的面积为 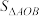 ,证明:
,证明: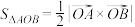 .
.
(3)证明: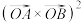 的几何意义表示以
的几何意义表示以 为底面、
为底面、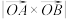 为高的三棱锥体积的
为高的三棱锥体积的 倍.
倍.
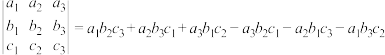
 若
若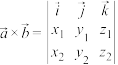 ,则称
,则称 为空间向量
为空间向量 与
与 的叉乘,其中
的叉乘,其中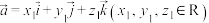 ,
,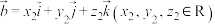 ,
, 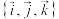 为单位正交基底. 以
为单位正交基底. 以  为坐标原点、分别以
为坐标原点、分别以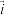 ,
, ,
,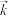 的方向为
的方向为  轴、
轴、  轴、
轴、  轴的正方向建立空间直角坐标系,已知
轴的正方向建立空间直角坐标系,已知 ,
, 是空间直角坐标系中异于
是空间直角坐标系中异于  的不同两点
的不同两点(1)①若
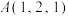 ,
, ,求
,求 ;
;②证明
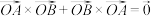 .
.(2)记
 的面积为
的面积为 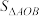 ,证明:
,证明: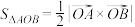 .
.(3)证明:
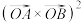 的几何意义表示以
的几何意义表示以 为底面、
为底面、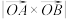 为高的三棱锥体积的
为高的三棱锥体积的 倍.
倍.
您最近一年使用:0次
2024-03-07更新
|
1049次组卷
|
8卷引用:河南省部分重点高中2024届高三普通高等学校招生全国统一考试(期末联考)数学试卷
河南省部分重点高中2024届高三普通高等学校招生全国统一考试(期末联考)数学试卷江苏省扬州市仪征中学2024届高三下学期期初调研测试数学试题 河南省部分重点高中(青桐鸣)2023-2024学年高三上学期期末大联考数学试题(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)江苏省江都中学2023-2024学年高二下学期3月联考数学试卷江苏省盱眙中学2023-2024学年高二下学期第一次学情调研数学试题(已下线)第七章 应用空间向量解立体几何问题拓展 专题二 平面法向量求法及其应用 微点2 平面法向量求法及其应用(二)【培优版】(已下线)专题08 期末必刷解答题专题训练的7种常考题型归类-期末真题分类汇编(北师大版2019必修第二册)
名校
解题方法
10 . 如图,在长方体 中,
中, ,点E为
,点E为 的中点,点F为侧面
的中点,点F为侧面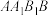 (含边界)上的动点,则下列说法
(含边界)上的动点,则下列说法
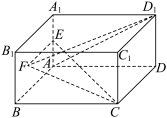
A.不存在点F,使得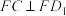 |
B.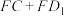 的最小值为 的最小值为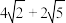 |
C.满足 的点F的轨迹长度为 的点F的轨迹长度为 |
D.若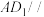 平面 平面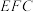 ,则线段 ,则线段 长度的最小值为 长度的最小值为 |
您最近一年使用:0次



