解题方法
1 . 已知 分别为双曲线
分别为双曲线 的左、右支上的点,
的左、右支上的点, 的右焦点为
的右焦点为 为坐标原点.
为坐标原点.
(1)若 三点共线,且
三点共线,且 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程.
(2)若直线 与圆
与圆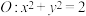 相切,试判断
相切,试判断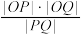 是否为定值.若是,求出该定值;若不是,请说明理由.
是否为定值.若是,求出该定值;若不是,请说明理由.
 分别为双曲线
分别为双曲线 的左、右支上的点,
的左、右支上的点, 的右焦点为
的右焦点为 为坐标原点.
为坐标原点.(1)若
 三点共线,且
三点共线,且 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程.(2)若直线
 与圆
与圆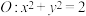 相切,试判断
相切,试判断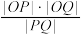 是否为定值.若是,求出该定值;若不是,请说明理由.
是否为定值.若是,求出该定值;若不是,请说明理由.
您最近一年使用:0次
2024-03-07更新
|
583次组卷
|
2卷引用:广东省2023-2024学年高三下学期百日冲刺检测数学试题
2 . 已知动点 与定点
与定点 的距离和
的距离和 到定直线
到定直线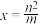 的距离的比为常数
的距离的比为常数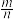 .其中
.其中 ,且
,且 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求 的方程,并说明轨迹的形状;
的方程,并说明轨迹的形状;
(2)设点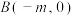 ,若曲线
,若曲线 上两动点
上两动点 均在
均在 轴上方,
轴上方, ,且
,且 与
与 相交于点
相交于点 .
.
①当 时,求证:
时,求证: 的值及
的值及 的周长均为定值;
的周长均为定值;
②当 时,记
时,记 的面积为
的面积为 ,其内切圆半径为
,其内切圆半径为 ,试探究是否存在常数
,试探究是否存在常数 ,使得
,使得 恒成立?若存在,求
恒成立?若存在,求 (用
(用 表示);若不存在,请说明理由.
表示);若不存在,请说明理由.
 与定点
与定点 的距离和
的距离和 到定直线
到定直线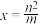 的距离的比为常数
的距离的比为常数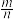 .其中
.其中 ,且
,且 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.(1)求
 的方程,并说明轨迹的形状;
的方程,并说明轨迹的形状;(2)设点
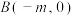 ,若曲线
,若曲线 上两动点
上两动点 均在
均在 轴上方,
轴上方, ,且
,且 与
与 相交于点
相交于点 .
.①当
 时,求证:
时,求证: 的值及
的值及 的周长均为定值;
的周长均为定值;②当
 时,记
时,记 的面积为
的面积为 ,其内切圆半径为
,其内切圆半径为 ,试探究是否存在常数
,试探究是否存在常数 ,使得
,使得 恒成立?若存在,求
恒成立?若存在,求 (用
(用 表示);若不存在,请说明理由.
表示);若不存在,请说明理由.
您最近一年使用:0次
2024-02-29更新
|
5208次组卷
|
7卷引用:广东省深圳市2024届高三第一次调研考试数学试卷
广东省深圳市2024届高三第一次调研考试数学试卷广东省广州市白云中学2023-2024学年高三下学期零模(3月月考)数学试题(已下线)黄金卷08(2024新题型)2024届河北省承德市部分高中二模数学试题河北省衡水市部分学校2024届高三下学期二模考试数学试题海南省海南中学2024届高三第一次模拟数学试题(已下线)数学(新高考卷02,新题型结构)
名校
3 . 抛物线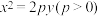 与椭圆
与椭圆 有相同的焦点,
有相同的焦点, 分别是椭圆的上、下焦点,P是椭圆上的任一点,I是
分别是椭圆的上、下焦点,P是椭圆上的任一点,I是 的内心,
的内心, 交y轴于M,且
交y轴于M,且 ,点
,点 是抛物线上在第一象限的点,且在该点处的切线与x轴的交点为
是抛物线上在第一象限的点,且在该点处的切线与x轴的交点为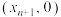 ,若
,若 ,则
,则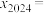
____________ .
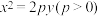 与椭圆
与椭圆 有相同的焦点,
有相同的焦点, 分别是椭圆的上、下焦点,P是椭圆上的任一点,I是
分别是椭圆的上、下焦点,P是椭圆上的任一点,I是 的内心,
的内心, 交y轴于M,且
交y轴于M,且 ,点
,点 是抛物线上在第一象限的点,且在该点处的切线与x轴的交点为
是抛物线上在第一象限的点,且在该点处的切线与x轴的交点为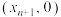 ,若
,若 ,则
,则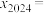
您最近一年使用:0次
2024-02-27更新
|
906次组卷
|
5卷引用:广东省华南师范大学附属中学2024届高三下学期模拟测试(一)数学试题
名校
4 . 多元导数在微积分学中有重要的应用.设 是由
是由 ,
, ,
, …等多个自变量唯一确定的因变量,则当
…等多个自变量唯一确定的因变量,则当 变化为
变化为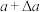 时,
时, 变化为
变化为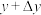 ,记
,记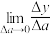 为
为 对
对 的导数,其符号为
的导数,其符号为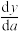 .和一般导数一样,若在
.和一般导数一样,若在 上,已知
上,已知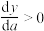 ,则
,则 随着
随着 的增大而增大;反之,已知
的增大而增大;反之,已知 ,则
,则 随着
随着 的增大而减小.多元导数除满足一般分式的运算性质外,还具有下列性质:①可加性:
的增大而减小.多元导数除满足一般分式的运算性质外,还具有下列性质:①可加性: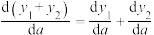 ;②乘法法则:
;②乘法法则: ;③除法法则:
;③除法法则: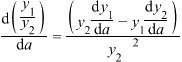 ;④复合法则:
;④复合法则: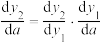 .记
.记 .(
.(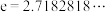 为自然对数的底数),
为自然对数的底数),
(1)写出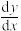 和
和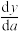 的表达式;
的表达式;
(2)已知方程 有两实根
有两实根 ,
, .
.
①求出 的取值范围;
的取值范围;
②证明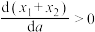 ,并写出
,并写出 随
随 的变化趋势.
的变化趋势.
 是由
是由 ,
, ,
, …等多个自变量唯一确定的因变量,则当
…等多个自变量唯一确定的因变量,则当 变化为
变化为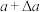 时,
时, 变化为
变化为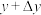 ,记
,记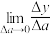 为
为 对
对 的导数,其符号为
的导数,其符号为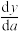 .和一般导数一样,若在
.和一般导数一样,若在 上,已知
上,已知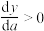 ,则
,则 随着
随着 的增大而增大;反之,已知
的增大而增大;反之,已知 ,则
,则 随着
随着 的增大而减小.多元导数除满足一般分式的运算性质外,还具有下列性质:①可加性:
的增大而减小.多元导数除满足一般分式的运算性质外,还具有下列性质:①可加性: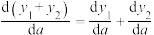 ;②乘法法则:
;②乘法法则: ;③除法法则:
;③除法法则: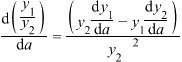 ;④复合法则:
;④复合法则: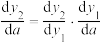 .记
.记 .(
.(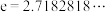 为自然对数的底数),
为自然对数的底数),(1)写出
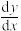 和
和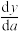 的表达式;
的表达式;(2)已知方程
 有两实根
有两实根 ,
, .
.①求出
 的取值范围;
的取值范围;②证明
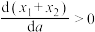 ,并写出
,并写出 随
随 的变化趋势.
的变化趋势.
您最近一年使用:0次
2024-02-21更新
|
1075次组卷
|
3卷引用:广东省广州市华南师范大学附属中学2024届高三上学期数学周测试题(12)
广东省广州市华南师范大学附属中学2024届高三上学期数学周测试题(12)(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编江苏省海安高级中学2023-2024学年高二下学期第二次月考数学试题
名校
5 . 已知函数 .
.
(1)讨论 的单调性;
的单调性;
(2)设 ,
, 分别为
分别为 的极大值点和极小值点,记
的极大值点和极小值点,记 ,
,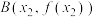 .
.
(ⅰ)证明:直线AB与曲线 交于另一点C;
交于另一点C;
(ⅱ)在(i)的条件下,判断是否存在常数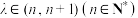 ,使得
,使得 .若存在,求n;若不存在,说明理由.
.若存在,求n;若不存在,说明理由.
附: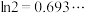 ,
,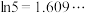 .
.
 .
.(1)讨论
 的单调性;
的单调性;(2)设
 ,
, 分别为
分别为 的极大值点和极小值点,记
的极大值点和极小值点,记 ,
,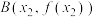 .
.(ⅰ)证明:直线AB与曲线
 交于另一点C;
交于另一点C;(ⅱ)在(i)的条件下,判断是否存在常数
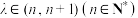 ,使得
,使得 .若存在,求n;若不存在,说明理由.
.若存在,求n;若不存在,说明理由.附:
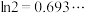 ,
,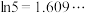 .
.
您最近一年使用:0次
2024-02-20更新
|
976次组卷
|
6卷引用:广东省东莞市第七高级中学2023-2024学年高二下学期数学第一次月考数学试题
名校
解题方法
6 . 在平面直角坐标系 中,点
中,点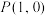 ,点A为动点,以线段
,点A为动点,以线段 为直径的圆与
为直径的圆与 轴相切,记A的轨迹为
轴相切,记A的轨迹为 ,直线
,直线 交
交 于另一点B.
于另一点B.
(1)求 的方程;
的方程;
(2) 的外接圆交
的外接圆交 于点
于点 (不与O,A,B重合),依次连接O,A,C,B构成凸四边形
(不与O,A,B重合),依次连接O,A,C,B构成凸四边形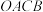 ,记其面积为
,记其面积为 .
.
(i)证明: 的重心在定直线上;
的重心在定直线上;
(ii)求 的取值范围.
的取值范围.
 中,点
中,点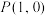 ,点A为动点,以线段
,点A为动点,以线段 为直径的圆与
为直径的圆与 轴相切,记A的轨迹为
轴相切,记A的轨迹为 ,直线
,直线 交
交 于另一点B.
于另一点B.(1)求
 的方程;
的方程;(2)
 的外接圆交
的外接圆交 于点
于点 (不与O,A,B重合),依次连接O,A,C,B构成凸四边形
(不与O,A,B重合),依次连接O,A,C,B构成凸四边形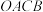 ,记其面积为
,记其面积为 .
.(i)证明:
 的重心在定直线上;
的重心在定直线上;(ii)求
 的取值范围.
的取值范围.
您最近一年使用:0次
2024-02-18更新
|
1672次组卷
|
3卷引用:广东省广州市培正中学2024届高三上学期第二次调研数学试题
22-23高三下·北京海淀·开学考试
名校
解题方法
7 . 若无穷数列 的各项均为整数.且对于
的各项均为整数.且对于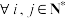 ,
, ,都存在
,都存在 ,使得
,使得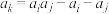 ,则称数列
,则称数列 满足性质P.
满足性质P.
(1)判断下列数列是否满足性质P,并说明理由.
① ,
, ,2,3,…;
,2,3,…;
②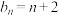 ,
, ,2,3,….
,2,3,….
(2)若数列 满足性质P,且
满足性质P,且 ,求证:集合
,求证:集合 为无限集;
为无限集;
(3)若周期数列 满足性质P,求数列
满足性质P,求数列 的通项公式.
的通项公式.
 的各项均为整数.且对于
的各项均为整数.且对于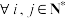 ,
, ,都存在
,都存在 ,使得
,使得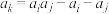 ,则称数列
,则称数列 满足性质P.
满足性质P.(1)判断下列数列是否满足性质P,并说明理由.
①
 ,
, ,2,3,…;
,2,3,…;②
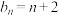 ,
, ,2,3,….
,2,3,….(2)若数列
 满足性质P,且
满足性质P,且 ,求证:集合
,求证:集合 为无限集;
为无限集;(3)若周期数列
 满足性质P,求数列
满足性质P,求数列 的通项公式.
的通项公式.
您最近一年使用:0次
2024-02-10更新
|
1552次组卷
|
14卷引用:广东省广州市执信中学2024届高三下学期教学情况检测(二)数学试题
广东省广州市执信中学2024届高三下学期教学情况检测(二)数学试题(已下线)北京市海淀区清华大学附属中学2023届高三下学期开学调研测试数学试题北京市第五中学2023届高三下学期3月检测数学试题北京市海淀区教师进修学校附属实验学校2023届高三零模数学试题北京市海淀区中国人民大学附属中学2022-2023学年高二下学期期中数学复习试题(2)(已下线)2023年北京高考数学真题变式题16-21北京市海淀区首都师范大学附属中学2023-2024学年高三上学期阶段练习(1月)数学试题北京市清华大学附属中学2023届高三下学期4月月考数学试题(已下线)北京市第四中学2023-2024学年高三下学期开学考试数学试题湖南省2024届高三数学新改革提高训练一(九省联考题型)2024届高三新改革数学模拟预测训练一(九省联考题型)湖南省张家界市民族中学2023-2024学年高二下学期入学考试数学试题(已下线)压轴题05数列压轴题15题型汇总-1北京市顺义区第一中学2024届高三下学期高考考前适应性检测数学试卷
8 . 已知动点 到直线
到直线 的距离与它到定点
的距离与它到定点 的距离之比为
的距离之比为 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求 的方程;
的方程;
(2)记 与
与 轴的上、下半轴的交点依次为
轴的上、下半轴的交点依次为 ,若
,若 为
为 上异于
上异于 的一点,且直线
的一点,且直线 分别交直线
分别交直线 于
于 两点,直线
两点,直线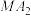 交
交 于点
于点 (异于
(异于 ).
).
(i)求直线 的斜率之积;
的斜率之积;
(ii)证明:直线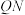 恒过定点.
恒过定点.
 到直线
到直线 的距离与它到定点
的距离与它到定点 的距离之比为
的距离之比为 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.(1)求
 的方程;
的方程;(2)记
 与
与 轴的上、下半轴的交点依次为
轴的上、下半轴的交点依次为 ,若
,若 为
为 上异于
上异于 的一点,且直线
的一点,且直线 分别交直线
分别交直线 于
于 两点,直线
两点,直线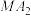 交
交 于点
于点 (异于
(异于 ).
).(i)求直线
 的斜率之积;
的斜率之积;(ii)证明:直线
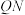 恒过定点.
恒过定点.
您最近一年使用:0次
解题方法
9 . 如图, 为圆锥
为圆锥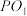 底面的直径,
底面的直径,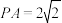 ,点
,点 是圆
是圆 上异于
上异于 的动点,球
的动点,球 内切于圆锥(与圆锥底面和侧面相切),点
内切于圆锥(与圆锥底面和侧面相切),点 是球
是球 与圆锥侧面的交线上的动点,则下列结论正确的是( )
与圆锥侧面的交线上的动点,则下列结论正确的是( )
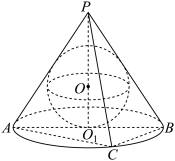
 为圆锥
为圆锥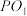 底面的直径,
底面的直径,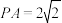 ,点
,点 是圆
是圆 上异于
上异于 的动点,球
的动点,球 内切于圆锥(与圆锥底面和侧面相切),点
内切于圆锥(与圆锥底面和侧面相切),点 是球
是球 与圆锥侧面的交线上的动点,则下列结论正确的是( )
与圆锥侧面的交线上的动点,则下列结论正确的是( )
A.若 ⊥ ⊥ ,三棱锥 ,三棱锥 体积的最大值为8 体积的最大值为8 |
B.若 ⊥ ⊥ ,平面 ,平面 与底面 与底面 所成角的取值范围为 所成角的取值范围为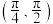 |
C.若 ,内切球 ,内切球 的表面积为 的表面积为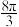 |
D.若 , , 的最大值为4 的最大值为4 |
您最近一年使用:0次
名校
解题方法
10 . 已知数列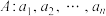 为有穷正整数数列.若数列A满足如下两个性质,则称数列A为m的k减数列:
为有穷正整数数列.若数列A满足如下两个性质,则称数列A为m的k减数列:
①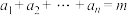 ;
;
②对于 ,使得
,使得 的正整数对
的正整数对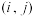 有k个.
有k个.
(1)写出所有4的1减数列;
(2)若存在m的6减数列,证明: ;
;
(3)若存在2024的k减数列,求k的最大值.
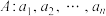 为有穷正整数数列.若数列A满足如下两个性质,则称数列A为m的k减数列:
为有穷正整数数列.若数列A满足如下两个性质,则称数列A为m的k减数列:①
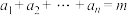 ;
;②对于
 ,使得
,使得 的正整数对
的正整数对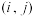 有k个.
有k个.(1)写出所有4的1减数列;
(2)若存在m的6减数列,证明:
 ;
;(3)若存在2024的k减数列,求k的最大值.
您最近一年使用:0次
2024-01-25更新
|
3791次组卷
|
9卷引用:2024届广东省新改革高三模拟高考预测卷一(九省联考题型)数学试卷
2024届广东省新改革高三模拟高考预测卷一(九省联考题型)数学试卷北京市通州区2024届高三上学期期末摸底考试数学试题江西省赣州市南康中学2024届高三“九省联考”考后模拟训练数学试题(一)安徽省合肥一六八中学2024届高三“九省联考”考后适应性测试数学试题(二)(已下线)(新高考新结构)2024年高考数学模拟卷(三)(已下线)信息必刷卷01湖南省长沙市雅礼中学2024届高三下学期数学月考试卷(八)(已下线)数学(江苏专用01)山东省日照市五莲县第一中学2024届高考模拟预测(一)数学试题



