名校
解题方法
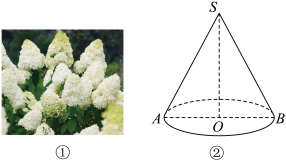
1 . 如图①所示,圆锥绣球是虎耳草科绣球属植物,在中国主要分布于西北、华东、华南、西南等地区,抗虫害能力强,其花序硕大,类似于圆锥形,因此得名.现将某圆锥绣球近似看作如图②所示的圆锥模型,已知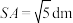 ,直线
,直线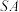 与圆锥底面所成角的余弦值为
与圆锥底面所成角的余弦值为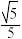 ,则该圆锥的侧面积为( )
,则该圆锥的侧面积为( )
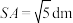 ,直线
,直线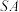 与圆锥底面所成角的余弦值为
与圆锥底面所成角的余弦值为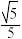 ,则该圆锥的侧面积为( )
,则该圆锥的侧面积为( )
A.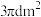 | B.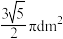 | C. | D. |
您最近半年使用:0次
2023-12-07更新
|
481次组卷
|
4卷引用:重庆市沙坪坝区第七中学校2024届高三上学期12月月考数学试题
名校
解题方法
2 . 如图,圆锥的母线长为2,点M为母线 的中点,从点M处拉一条绳子绕圆锥的侧面转一周到达B点,这条绳子的长度最短值为
的中点,从点M处拉一条绳子绕圆锥的侧面转一周到达B点,这条绳子的长度最短值为 ,则此圆锥的表面积为( )
,则此圆锥的表面积为( )
 的中点,从点M处拉一条绳子绕圆锥的侧面转一周到达B点,这条绳子的长度最短值为
的中点,从点M处拉一条绳子绕圆锥的侧面转一周到达B点,这条绳子的长度最短值为 ,则此圆锥的表面积为( )
,则此圆锥的表面积为( )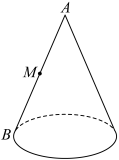
A. | B.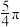 | C. | D. |
您最近半年使用:0次
2023-11-28更新
|
514次组卷
|
5卷引用:重庆市长寿中学校2023-2024学年高一下学期学段考试一(4月)试题
重庆市长寿中学校2023-2024学年高一下学期学段考试一(4月)试题山东省实验中学2024届学年高三第二次诊断考试数学试题(已下线)模块五 全真模拟篇 基础1 期末终极研习室(2023-2024学年第一学期)高三(已下线)专题8.3 简单几何体的表面积与体积-举一反三系列(人教A版2019必修第二册)(已下线)专题06 立体几何 第二讲 立体几何中的计算问题(分层练)
名校
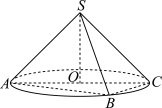
3 . 如图,圆锥 的底面圆
的底面圆 的直径
的直径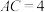 ,母线长为
,母线长为 ,点
,点 是圆
是圆 上异于
上异于 ,
, 的动点,则下列结论正确的是( )
的动点,则下列结论正确的是( )
 的底面圆
的底面圆 的直径
的直径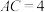 ,母线长为
,母线长为 ,点
,点 是圆
是圆 上异于
上异于 ,
, 的动点,则下列结论正确的是( )
的动点,则下列结论正确的是( )
A. 与底面所成角为45° 与底面所成角为45° |
B.圆锥 的表面积为 的表面积为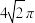 |
C.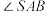 的取值范围是 的取值范围是 |
D.若点 为弧 为弧 的中点,则二面角 的中点,则二面角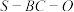 的平面角大小为45° 的平面角大小为45° |
您最近半年使用:0次
2023-10-30更新
|
1874次组卷
|
6卷引用:重庆市北碚区西南大学附中2024届高三上学期11月模拟测试数学试题
4 . 如图,在正三棱柱 中,
中,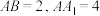 ,点
,点 是
是 的中点.
的中点.
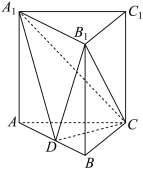
(1)求正三棱柱 的表面积;
的表面积;
(2)求三棱锥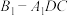 的体积.
的体积.
 中,
中,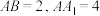 ,点
,点 是
是 的中点.
的中点.
(1)求正三棱柱
 的表面积;
的表面积;(2)求三棱锥
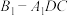 的体积.
的体积.
您最近半年使用:0次
名校
解题方法
5 . 已知圆锥的底面半径为1,侧面积为 ,则此圆锥的体积是
,则此圆锥的体积是___________ .
 ,则此圆锥的体积是
,则此圆锥的体积是
您最近半年使用:0次
2023-09-28更新
|
583次组卷
|
3卷引用:重庆市巴蜀中学校2023-2024学年高二上学期10月月考数学试题
名校
解题方法
6 . 已知正四棱柱 的每个顶点都在球
的每个顶点都在球 的球面上,若球
的球面上,若球 的表面积为
的表面积为 ,则该四棱柱的侧面积的最大值为
,则该四棱柱的侧面积的最大值为___________ .
 的每个顶点都在球
的每个顶点都在球 的球面上,若球
的球面上,若球 的表面积为
的表面积为 ,则该四棱柱的侧面积的最大值为
,则该四棱柱的侧面积的最大值为
您最近半年使用:0次
2023-09-21更新
|
294次组卷
|
2卷引用:重庆市2024届高三上学期9月月度质量检测数学试题
7 . 阿基米德是古时候伟大的古希腊数学家,他和高斯、牛顿并称为世界三大数学家,他一生最为满意的数学发现就是“圆柱容球”定理,即圆柱容器里放了一个球,该球顶天立地,四周碰边(即球与圆柱形容器的底面和侧面都相切),球的体积是圆柱体积的三分之二,球的表面积也是圆柱表面积的三分之二.今有一“圆柱容球”模型,其圆柱表面积为 ,则该模型中圆柱的体积与球的体积之和为( )
,则该模型中圆柱的体积与球的体积之和为( )
 ,则该模型中圆柱的体积与球的体积之和为( )
,则该模型中圆柱的体积与球的体积之和为( )A.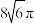 | B.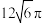 | C.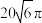 | D.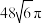 |
您最近半年使用:0次
名校
解题方法
8 . 已知圆锥顶点为 ,底面圆
,底面圆 的直径
的直径 长为
长为 ,
,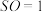 .若
.若 为底面圆周上不同于
为底面圆周上不同于 ,
, 的任意一点,则下列说法中正确的是( )
的任意一点,则下列说法中正确的是( )
A.圆锥 的侧面积为 的侧面积为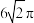 |
B. 面积的最大值为 面积的最大值为 |
C.圆锥 的外接球的表面积为 的外接球的表面积为 |
D.若圆锥的底面水平放置,且可从顶点向圆锥注水,当水的平面过 的中点时,则水的体积为 的中点时,则水的体积为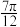 |
您最近半年使用:0次
2023-08-10更新
|
383次组卷
|
3卷引用:重庆市2024届高三上学期8月月度质量检测数学试题
名校
9 . 已知正三棱锥 的四个顶点在球
的四个顶点在球 的球面上,E,F分别是PA,AB的中点,
的球面上,E,F分别是PA,AB的中点, 且
且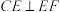 ,与该三棱锥的四个面都相切的球记为球
,与该三棱锥的四个面都相切的球记为球 ,则( )
,则( )
 的四个顶点在球
的四个顶点在球 的球面上,E,F分别是PA,AB的中点,
的球面上,E,F分别是PA,AB的中点, 且
且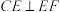 ,与该三棱锥的四个面都相切的球记为球
,与该三棱锥的四个面都相切的球记为球 ,则( )
,则( )A.三棱锥 的表面积为 的表面积为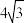 | B.球 的表面积为 的表面积为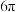 |
C.球 的体积为 的体积为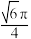 | D.球 的半径为 的半径为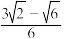 |
您最近半年使用:0次
2023-08-02更新
|
554次组卷
|
4卷引用:重庆市万州第二高级中学2024届高三上学期8月月考数学试题
解题方法
10 . 已知圆台上、下底面半径分别为1,2,侧面积为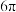 ,则这个圆台的体积为( )
,则这个圆台的体积为( )
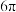 ,则这个圆台的体积为( )
,则这个圆台的体积为( )A.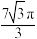 | B.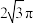 | C.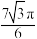 | D.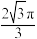 |
您最近半年使用:0次



