东北三省部分学校2024届高三下学期押题考试(二)数学试卷
全国
高三
二模
2024-06-09
640次
整体难度:
适中
考查范围:
复数、集合与常用逻辑用语、等式与不等式、函数与导数、计数原理与概率统计、三角函数与解三角形、平面解析几何、数列、空间向量与立体几何
东北三省部分学校2024届高三下学期押题考试(二)数学试卷
全国
高三
二模
2024-06-09
640次
整体难度:
适中
考查范围:
复数、集合与常用逻辑用语、等式与不等式、函数与导数、计数原理与概率统计、三角函数与解三角形、平面解析几何、数列、空间向量与立体几何
一、单选题 添加题型下试题
单选题
|
较易(0.85)
2. 已知集合A,B,若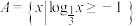 ,且
,且 ,则集合B可以为( )
,则集合B可以为( )
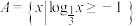 ,且
,且 ,则集合B可以为( )
,则集合B可以为( )A.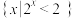 | B.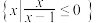 | C.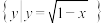 | D. |
您最近一年使用:0次
单选题
|
容易(0.94)
3. 在某短视频平台,某短视频发布者在最近一周内“粉丝”的增长数量绘制成如下折线图,则本周内“粉丝”增长数的中位数是( )
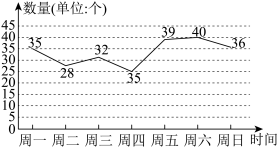
| A.26 | B.35 | C.36.5 | D.37 |
【知识点】 频率分布折线图的实际应用解读 计算几个数的中位数解读
您最近一年使用:0次
单选题
|
适中(0.65)
名校
解题方法
4. 已知角 的顶点与坐标原点重合,始边点x轴的非负半轴重合,终边上一点的坐标为
的顶点与坐标原点重合,始边点x轴的非负半轴重合,终边上一点的坐标为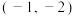 ,则
,则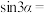 ( )
( )
 的顶点与坐标原点重合,始边点x轴的非负半轴重合,终边上一点的坐标为
的顶点与坐标原点重合,始边点x轴的非负半轴重合,终边上一点的坐标为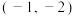 ,则
,则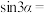 ( )
( )A.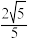 | B.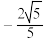 | C.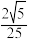 | D.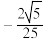 |
您最近一年使用:0次
2024-06-03更新
|
763次组卷
|
3卷引用:东北三省部分学校2024届高三下学期押题考试(二)数学试卷
单选题
|
适中(0.65)
5. 已知点P为抛物线 上一点,过点P作圆C:
上一点,过点P作圆C: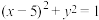 的两条切线,切点分别为M,N,则
的两条切线,切点分别为M,N,则 的最小值为( )
的最小值为( )
 上一点,过点P作圆C:
上一点,过点P作圆C: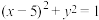 的两条切线,切点分别为M,N,则
的两条切线,切点分别为M,N,则 的最小值为( )
的最小值为( )A.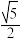 | B. | C.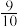 | D. |
【知识点】 二倍角的余弦公式解读 切线长 抛物线上的点到定点的距离及最值
您最近一年使用:0次
单选题
|
适中(0.65)
解题方法
6. 已知函数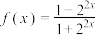 ,
,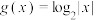 ,如图为函数
,如图为函数 的图象,则
的图象,则 可能为( )
可能为( )
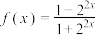 ,
,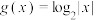 ,如图为函数
,如图为函数 的图象,则
的图象,则 可能为( )
可能为( )
A.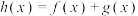 | B. |
C.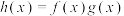 | D.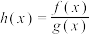 |
【知识点】 函数奇偶性的定义与判断解读 函数图像的识别
您最近一年使用:0次
2024-06-03更新
|
472次组卷
|
2卷引用:2024届广西普通高等学校招生押题卷(一)数学试题
单选题
|
适中(0.65)
解题方法
7. 在△ABC中,内角A,B,C所对的边分别为a,b,c,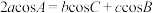 ,且
,且 ,则△ABC周长的最大值为( )
,则△ABC周长的最大值为( )
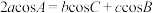 ,且
,且 ,则△ABC周长的最大值为( )
,则△ABC周长的最大值为( )A. | B. | C.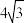 | D. |
您最近一年使用:0次
二、多选题 添加题型下试题
多选题
|
适中(0.65)
9. 已知圆O: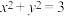 经过椭圆C:
经过椭圆C: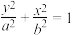 (
( )的两个焦点
)的两个焦点 ,
, ,且P为圆O与椭圆C在第一象限内的公共点,且
,且P为圆O与椭圆C在第一象限内的公共点,且 的面积为1,则下列结论正确的是( )
的面积为1,则下列结论正确的是( )
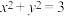 经过椭圆C:
经过椭圆C: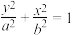 (
( )的两个焦点
)的两个焦点 ,
, ,且P为圆O与椭圆C在第一象限内的公共点,且
,且P为圆O与椭圆C在第一象限内的公共点,且 的面积为1,则下列结论正确的是( )
的面积为1,则下列结论正确的是( )| A.椭圆C的长轴长为2 | B.椭圆C的短轴长为2 |
C.椭圆C的离心率为 | D.点P的坐标为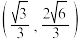 |
您最近一年使用:0次
多选题
|
适中(0.65)
名校
解题方法
10. 甲、乙两个不透明的袋子中分别装两种颜色不同但是大小相同的小球,甲袋中装有3个红球和4个绿球;乙袋中装有5个红球和2个绿球.先从甲袋中随机摸出一个小球放入乙袋中,再从乙袋中随机获出一个小球,记 表示事件“从甲袋摸出的是红球”,
表示事件“从甲袋摸出的是红球”, 表示事件“从甲袋摸出的是绿球”,记
表示事件“从甲袋摸出的是绿球”,记 表示事件“从乙袋摸出的是红球”,
表示事件“从乙袋摸出的是红球”, 表示事件“从乙袋摸出的是绿球”,则下列说法正确的是( )
表示事件“从乙袋摸出的是绿球”,则下列说法正确的是( )
 表示事件“从甲袋摸出的是红球”,
表示事件“从甲袋摸出的是红球”, 表示事件“从甲袋摸出的是绿球”,记
表示事件“从甲袋摸出的是绿球”,记 表示事件“从乙袋摸出的是红球”,
表示事件“从乙袋摸出的是红球”, 表示事件“从乙袋摸出的是绿球”,则下列说法正确的是( )
表示事件“从乙袋摸出的是绿球”,则下列说法正确的是( )A. , , 是对立事件 是对立事件 | B. , , 是独立事件 是独立事件 |
C.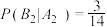 | D. |
您最近一年使用:0次
2024-06-11更新
|
510次组卷
|
2卷引用:东北三省部分学校2024届高三下学期押题考试(二)数学试卷
多选题
|
较难(0.4)
11. 已知函数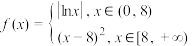 ,函数
,函数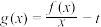 (
( )的零点记为
)的零点记为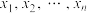 ,
, ,则( )
,则( )
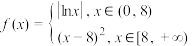 ,函数
,函数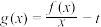 (
( )的零点记为
)的零点记为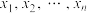 ,
, ,则( )
,则( )| A.n的最小值为2 | B.n的最大值为4 |
C.当 时,t的最大值为 时,t的最大值为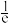 | D.当 时,t的最大值为 时,t的最大值为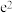 |
您最近一年使用:0次
三、填空题 添加题型下试题
填空题-单空题
|
较易(0.85)
您最近一年使用:0次
填空题-单空题
|
较难(0.4)
名校
14. 已知长方体 的底面ABCD为边长是2的正方形,
的底面ABCD为边长是2的正方形, ,E,F分别为棱AB,
,E,F分别为棱AB, 的中点,则过
的中点,则过 ,E,F的平面截长方体
,E,F的平面截长方体 的表面所得截面的面积为
的表面所得截面的面积为______________ .
 的底面ABCD为边长是2的正方形,
的底面ABCD为边长是2的正方形, ,E,F分别为棱AB,
,E,F分别为棱AB, 的中点,则过
的中点,则过 ,E,F的平面截长方体
,E,F的平面截长方体 的表面所得截面的面积为
的表面所得截面的面积为
您最近一年使用:0次
2024-06-03更新
|
638次组卷
|
5卷引用:东北三省部分学校2024届高三下学期押题考试(二)数学试卷
东北三省部分学校2024届高三下学期押题考试(二)数学试卷河南省漯河市高级中学2024届高三下学期三模数学试题广东省广州市广东实验中学2024届高三教学情况测试(一)河南省许昌市许昌高级中学2024届高三下学期三模数学试题(已下线)第02讲 空间点、直线、平面之间的位置关系(六大题型)(练习)
四、解答题 添加题型下试题
解答题-问答题
|
较易(0.85)
解题方法
15. 已知数列 的前n项和为
的前n项和为 ,且
,且 ,
,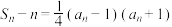 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前n项和为
的前n项和为 .
.
 的前n项和为
的前n项和为 ,且
,且 ,
,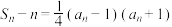 .
.(1)求数列
 的通项公式;
的通项公式;(2)求数列
 的前n项和为
的前n项和为 .
.
您最近一年使用:0次
解答题-证明题
|
适中(0.65)
名校
解题方法
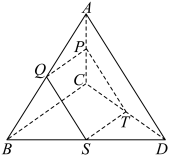
16. 如图,在正三棱锥 中,
中,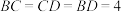 ,点
,点 满足
满足 ,
,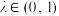 ,过点
,过点 作平面
作平面 分别与棱AB,BD,CD交于Q,S,T三点,且
分别与棱AB,BD,CD交于Q,S,T三点,且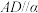 ,
, .
.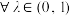 ,四边形
,四边形 总是矩形;
总是矩形;
(2)若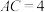 ,求四棱锥
,求四棱锥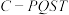 体积的最大值.
体积的最大值.
 中,
中,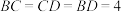 ,点
,点 满足
满足 ,
,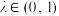 ,过点
,过点 作平面
作平面 分别与棱AB,BD,CD交于Q,S,T三点,且
分别与棱AB,BD,CD交于Q,S,T三点,且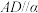 ,
, .
.
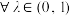 ,四边形
,四边形 总是矩形;
总是矩形;(2)若
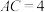 ,求四棱锥
,求四棱锥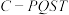 体积的最大值.
体积的最大值.
您最近一年使用:0次
2024-04-15更新
|
805次组卷
|
3卷引用:河北省沧州市盐山中学等校2024届高三下学期一模联考数学试题
解答题-问答题
|
适中(0.65)
解题方法
17. 流感病毒是一种RNA病毒,其遗传物质是RNA,它还有个蛋白质包膜,上面有各种突起.流感病毒大致分为甲型、乙型、丙型三种,分别能引起甲型流感、乙型流感和丙型流感,其中甲流病毒带来的危害最大.禽流感、猪流感、H7N9、H5N1等都是甲流病毒引起的.甲流病毒传染性最强,致死率最高.乙流病毒目前只有山形株和维多利亚株两种类型,传播性没有甲流病毒那么强,乙流危害性远不及甲流.丙流病毒传播比较少,发病率也比较低,只比普通感冒麻烦一点.某药品科技研发团队针对甲流病毒的特点,研发出预防甲流药品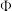 和治疗甲流药品
和治疗甲流药品 ,根据研发前期对动物试验所获得的相关有效数据作出统计,随机选取其中的100个样本数据,得到如下2×2联联表:
,根据研发前期对动物试验所获得的相关有效数据作出统计,随机选取其中的100个样本数据,得到如下2×2联联表:
(1)根据 的独立性检验,分析预防药品
的独立性检验,分析预防药品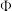 对预防甲流的有效性;
对预防甲流的有效性;
(2)用频率估计概率(保留一位有效数字),从已经感染的动物中,采用随机抽样方式每次选出1只,用治疗药品 对该动物进行治疗,已知治疗药品
对该动物进行治疗,已知治疗药品 的治愈数据如下:对未使用过预防药品
的治愈数据如下:对未使用过预防药品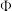 的动物的治愈率为0.5,对使用过预防药品
的动物的治愈率为0.5,对使用过预防药品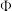 的动物的治愈率为0.75,若共选取3只已感染动物,每次选取的结果相互独立,记选取的3只已感染动物中被治愈的动物只数为X,求X的分布列与数学期望.
的动物的治愈率为0.75,若共选取3只已感染动物,每次选取的结果相互独立,记选取的3只已感染动物中被治愈的动物只数为X,求X的分布列与数学期望.
附: ,
, .
.
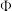 和治疗甲流药品
和治疗甲流药品 ,根据研发前期对动物试验所获得的相关有效数据作出统计,随机选取其中的100个样本数据,得到如下2×2联联表:
,根据研发前期对动物试验所获得的相关有效数据作出统计,随机选取其中的100个样本数据,得到如下2×2联联表:预防药品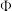 | 感染 | 未感染 | 合计 |
| 未使用 | 22 | 23 | 45 |
| 使用 | 16 | 39 | 55 |
| 合计 | 38 | 62 | 100 |
 的独立性检验,分析预防药品
的独立性检验,分析预防药品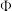 对预防甲流的有效性;
对预防甲流的有效性;(2)用频率估计概率(保留一位有效数字),从已经感染的动物中,采用随机抽样方式每次选出1只,用治疗药品
 对该动物进行治疗,已知治疗药品
对该动物进行治疗,已知治疗药品 的治愈数据如下:对未使用过预防药品
的治愈数据如下:对未使用过预防药品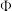 的动物的治愈率为0.5,对使用过预防药品
的动物的治愈率为0.5,对使用过预防药品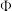 的动物的治愈率为0.75,若共选取3只已感染动物,每次选取的结果相互独立,记选取的3只已感染动物中被治愈的动物只数为X,求X的分布列与数学期望.
的动物的治愈率为0.75,若共选取3只已感染动物,每次选取的结果相互独立,记选取的3只已感染动物中被治愈的动物只数为X,求X的分布列与数学期望.附:
 ,
, .
. | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
您最近一年使用:0次
18. 已知双曲线 :
: (
( )经过点
)经过点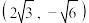 和
和 ,
, ,
,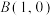 ,
, ,
, 分别在双曲线
分别在双曲线 的左、右两支上,
的左、右两支上, 为双曲线左支上一点,且
为双曲线左支上一点,且 ,
, ,
, 三点共线,
三点共线, ,
, ,
, 三点共线,直线
三点共线,直线 ,
, 的斜率分别记为
的斜率分别记为 ,
, .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)求证: 为定值;
为定值;
(3)试判断直线 是否过定点,若是,请求出定点坐标,若不是,请说明理由.
是否过定点,若是,请求出定点坐标,若不是,请说明理由.
 :
: (
( )经过点
)经过点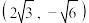 和
和 ,
, ,
,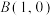 ,
, ,
, 分别在双曲线
分别在双曲线 的左、右两支上,
的左、右两支上, 为双曲线左支上一点,且
为双曲线左支上一点,且 ,
, ,
, 三点共线,
三点共线, ,
, ,
, 三点共线,直线
三点共线,直线 ,
, 的斜率分别记为
的斜率分别记为 ,
, .
.(1)求双曲线
 的标准方程;
的标准方程;(2)求证:
 为定值;
为定值;(3)试判断直线
 是否过定点,若是,请求出定点坐标,若不是,请说明理由.
是否过定点,若是,请求出定点坐标,若不是,请说明理由.
您最近一年使用:0次
2024-06-03更新
|
345次组卷
|
6卷引用:东北三省部分学校2024届高三下学期押题考试(二)数学试卷
东北三省部分学校2024届高三下学期押题考试(二)数学试卷(已下线)专题10 解析几何中的定点问题【练】(压轴大全)云南省昭通市第一中学教研联盟2023-2024学年高二下学期7月期末质量检测数学试题(B卷)(已下线)压轴题08 圆锥曲线综合的5大常考类型-【常考压轴题】(人教B版2019选择性必修第一册)(已下线)模块二 专题2 解析几何中定值、定点、定直线问题【练】(高二期中压轴专项)(已下线)专题1 特殊探路 直接求解(经典好题母题)【练】
解答题-证明题
|
较难(0.4)
名校
19. 对于函数 ,
, ,若存在
,若存在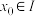 ,使得
,使得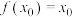 ,则称
,则称 为函数
为函数 的一阶不动点;若存在
的一阶不动点;若存在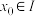 ,使得
,使得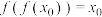 ,则称
,则称 为函数
为函数 的二阶不动点;依此类推,可以定义函数
的二阶不动点;依此类推,可以定义函数 的
的 阶不动点.其中一阶不动点简称为“不动点”,二阶不动点简称为“稳定点”,函数
阶不动点.其中一阶不动点简称为“不动点”,二阶不动点简称为“稳定点”,函数 的“不动点”和“稳定点”构成的集合分别记为
的“不动点”和“稳定点”构成的集合分别记为 和
和 ,即
,即 ,
,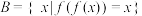 .
.
(1)若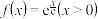 ,证明:集合
,证明:集合 中有且仅有一个元素;
中有且仅有一个元素;
(2)若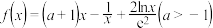 ,讨论集合
,讨论集合 的子集的个数.
的子集的个数.
 ,
, ,若存在
,若存在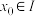 ,使得
,使得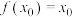 ,则称
,则称 为函数
为函数 的一阶不动点;若存在
的一阶不动点;若存在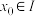 ,使得
,使得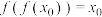 ,则称
,则称 为函数
为函数 的二阶不动点;依此类推,可以定义函数
的二阶不动点;依此类推,可以定义函数 的
的 阶不动点.其中一阶不动点简称为“不动点”,二阶不动点简称为“稳定点”,函数
阶不动点.其中一阶不动点简称为“不动点”,二阶不动点简称为“稳定点”,函数 的“不动点”和“稳定点”构成的集合分别记为
的“不动点”和“稳定点”构成的集合分别记为 和
和 ,即
,即 ,
,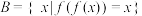 .
.(1)若
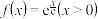 ,证明:集合
,证明:集合 中有且仅有一个元素;
中有且仅有一个元素;(2)若
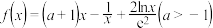 ,讨论集合
,讨论集合 的子集的个数.
的子集的个数.
【知识点】 利用导数研究函数的零点 函数新定义
您最近一年使用:0次
2024-04-15更新
|
458次组卷
|
4卷引用:河北省沧州市盐山中学等校2024届高三下学期一模联考数学试题
河北省沧州市盐山中学等校2024届高三下学期一模联考数学试题东北三省部分学校2024届高三下学期押题考试(二)数学试卷安徽省皖北县中联盟(省重点高中)2023-2024学年高二下学期期中数学试题(已下线)专题2 函数与导数新定义压轴大题(二)【讲】
试卷分析
导出
整体难度:适中
考查范围:复数、集合与常用逻辑用语、等式与不等式、函数与导数、计数原理与概率统计、三角函数与解三角形、平面解析几何、数列、空间向量与立体几何
试卷题型(共 19题)
题型
数量
单选题
8
多选题
3
填空题
3
解答题
5
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 复数的相等 复数加减法的代数运算 共轭复数的概念及计算 | |
| 2 | 0.85 | 交集的概念及运算 分式不等式 由指数函数的单调性解不等式 由对数函数的单调性解不等式 | |
| 3 | 0.94 | 频率分布折线图的实际应用 计算几个数的中位数 | |
| 4 | 0.65 | 由终边或终边上的点求三角函数值 用和、差角的余弦公式化简、求值 二倍角的正弦公式 二倍角的余弦公式 | |
| 5 | 0.65 | 二倍角的余弦公式 切线长 抛物线上的点到定点的距离及最值 | |
| 6 | 0.65 | 函数奇偶性的定义与判断 函数图像的识别 | |
| 7 | 0.65 | 辅助角公式 正弦定理边角互化的应用 求三角形中的边长或周长的最值或范围 | |
| 8 | 0.85 | 根据数列递推公式写出数列的项 等比数列的定义 | |
| 二、多选题 | |||
| 9 | 0.65 | 求椭圆的长轴、短轴 求椭圆的离心率或离心率的取值范围 椭圆中三角形(四边形)的面积 | |
| 10 | 0.65 | 判断所给事件是否是互斥关系 计算条件概率 独立事件的乘法公式 | |
| 11 | 0.4 | 求曲线切线的斜率(倾斜角) 基本初等函数的导数公式 求函数零点或方程根的个数 | |
| 三、填空题 | |||
| 12 | 0.85 | 求指定项的系数 | 单空题 |
| 13 | 0.94 | 求cosx型三角函数的单调性 | 单空题 |
| 14 | 0.4 | 判断正方体的截面形状 由平面的基本性质作截面图形 面面平行证明线线平行 | 单空题 |
| 四、解答题 | |||
| 15 | 0.85 | 利用定义求等差数列通项公式 求等比数列前n项和 分组(并项)法求和 利用an与sn关系求通项或项 | 问答题 |
| 16 | 0.65 | 由导数求函数的最值(不含参) 锥体体积的有关计算 面面垂直证线面垂直 线面平行的性质 | 证明题 |
| 17 | 0.65 | 独立性检验解决实际问题 利用二项分布求分布列 二项分布的均值 利用全概率公式求概率 | 问答题 |
| 18 | 0.4 | 根据双曲线过的点求标准方程 双曲线中的直线过定点问题 双曲线中的定值问题 | 证明题 |
| 19 | 0.4 | 利用导数研究函数的零点 函数新定义 | 证明题 |

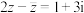 ,则
,则 (
(



 ,
, ,且
,且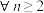 ,
, ,则(
,则(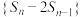 是等比数列
是等比数列


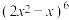 的展开式中,
的展开式中, 的系数为
的系数为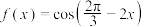 ,
,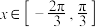 ,则函数
,则函数 的单调递减区间为
的单调递减区间为

