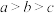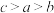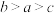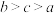江苏省南京大学附属中学2020-2021学年高三上学期第一次阶段检测数学试题
江苏
高三
阶段练习
2020-10-19
617次
整体难度:
容易
考查范围:
集合与常用逻辑用语、等式与不等式、函数与导数、计数原理与概率统计、三角函数与解三角形、空间向量与立体几何、数列、平面解析几何
一、单选题 添加题型下试题
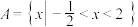 ,
, ,则
,则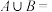 ( )
( )A. | B.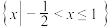 |
C.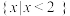 | D.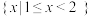 |
【知识点】 并集的概念及运算解读 解不含参数的一元二次不等式解读
 的图像与
的图像与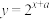 的图像关于直线
的图像关于直线 对称,且
对称,且 ,则
,则
A. | B. | C. | D. |
【知识点】 函数对称性的应用
 个小灯,另种是大灯下缀
个小灯,另种是大灯下缀 个小灯,大灯共
个小灯,大灯共 个,小灯共
个,小灯共 个.若在这座楼阁的灯球中,随机选取两个灯球,则至少有一个灯球是大灯下缀
个.若在这座楼阁的灯球中,随机选取两个灯球,则至少有一个灯球是大灯下缀 个小灯的概率为( )
个小灯的概率为( )A.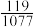 | B.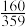 | C.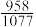 | D.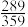 |
【知识点】 根据古典概型的概率求参数
 为R上的可导函数,当
为R上的可导函数,当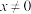 时,
时,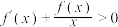 ,若
,若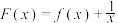 ,则函数
,则函数 的零点个数为( )
的零点个数为( )| A.0 | B.1 | C.2 | D.0或2 |
【知识点】 利用导数研究函数的零点
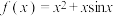 的图象大致为( )
的图象大致为( )A.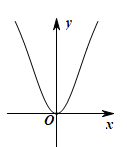 | B.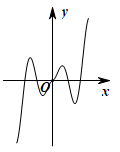 |
C. | D. |
【知识点】 函数奇偶性的应用 函数图像的识别 用导数判断或证明已知函数的单调性
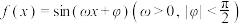 的图象如图所示,为了得到
的图象如图所示,为了得到 的图象,只需将
的图象,只需将 的图象( )
的图象( )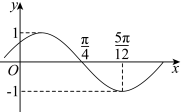
A.向右平移 个单位长度 个单位长度 | B.向左平移 个单位长度 个单位长度 |
C.向右平移 个单位长度 个单位长度 | D.向左平移 个单位长度 个单位长度 |
【知识点】 描述正(余)弦型函数图象的变换过程解读
| A.8号学生 | B.200号学生 | C.616号学生 | D.815号学生 |
【知识点】 系统抽样
二、多选题 添加题型下试题
 ,
, ,下列四个结论正确的是( )
,下列四个结论正确的是( )A. 的图象向左平移 的图象向左平移 个单位长度,即可得到 个单位长度,即可得到 的图象 的图象 |
B.当 时,函数 时,函数 取得最大值 取得最大值 |
C.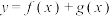 图象的对称中心是 图象的对称中心是 , ,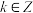 |
D.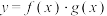 在区间 在区间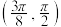 上单调递增 上单调递增 |
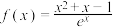 ,则下列结论正确的是( )
,则下列结论正确的是( )A.函数 存在两个不同的零点 存在两个不同的零点 |
B.函数 既存在极大值又存在极小值 既存在极大值又存在极小值 |
C.当 时,方程 时,方程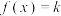 有且只有两个实根 有且只有两个实根 |
D.若 时, 时,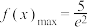 ,则 ,则 的最小值为 的最小值为 |
 中,
中, ,
, ,
, 分别为棱
分别为棱 ,
, 的中点,则下列说法正确的是( )
的中点,则下列说法正确的是( )
A. 四点共面 四点共面 | B.直线 与 与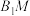 所成角的为 所成角的为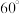 |
C. 平面 平面 | D.平面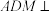 平面 平面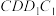 |
【知识点】 空间中的点(线)共面问题 求异面直线所成的角 判断线面平行 判断面面是否垂直
 ,
,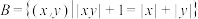 ,若
,若 是平面上正八边形的顶点所构成的集合,则下列说法正确的为( )
是平面上正八边形的顶点所构成的集合,则下列说法正确的为( )
| A.a的值可为2 | B.a的值可为 |
C.a的值可为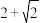 | D.a的值可为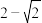 |
【知识点】 根据交集结果求集合或参数解读
三、填空题 添加题型下试题
 ,
,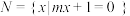 ,且
,且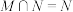 ,则实数
,则实数 的值为
的值为【知识点】 根据交集结果求集合或参数解读
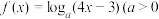 且
且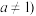 的图象所过定点的坐标是
的图象所过定点的坐标是【知识点】 对数型函数图象过定点问题
【知识点】 等差数列的简单应用
 的离心率为2,则此双曲线的渐近线方程
的离心率为2,则此双曲线的渐近线方程四、解答题 添加题型下试题
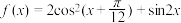 .
.(1)若
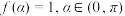 ,求
,求 的值;
的值;(2)求
 的单调增区间.
的单调增区间.
 平面ABCD,
平面ABCD, ,
,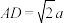 点E是
点E是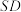 上的点,且
上的点,且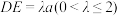
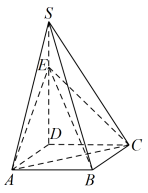
(1)求证:对任意的
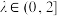 ,都有
,都有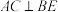
(2)设二面角C—AE—D的大小为

 ,直线BE与平面ABCD所成的角为
,直线BE与平面ABCD所成的角为 ,若
,若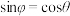 ,求
,求 的值
的值
【知识点】 空间位置关系的向量证明 线面角的向量求法 面面角的向量求法
 ,
,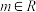 ,
, .
.(1)讨论
 的单调区间;
的单调区间;(2)若
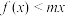 恒成立,求
恒成立,求 的取值范围.
的取值范围.

| 男性 | 女性 | 合计 | |
| 手机支付族 | |||
| 非手机支付族 | |||
| 合计 |
(2)用样本估计总体,若从腾讯服务的用户中随机抽取3位女性用户,这3位用户中“手机支付族”的人数为
 ,求随机变量
,求随机变量 的期望;
的期望;(3)某商场为了推广手机支付,特推出两种优惠方案,方案一:手机支付消费每满1000元可直减100元;方案二:手机支付消费每满1000元可抽奖2次,每次中奖的概率同为
 ,且每次抽奖互不影响,中奖一次打9折,中奖两次打8.5折.如果你打算用手机支付购买某样价值1200元的商品,请从实际付款金额的数学期望的角度分析,选择哪种优惠方案更划算?
,且每次抽奖互不影响,中奖一次打9折,中奖两次打8.5折.如果你打算用手机支付购买某样价值1200元的商品,请从实际付款金额的数学期望的角度分析,选择哪种优惠方案更划算?附:

| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
【知识点】 独立性检验解决实际问题解读 二项分布的均值解读
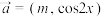 ,
,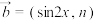 ,设函数
,设函数 ,且
,且 的图象过点
的图象过点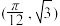 和点
和点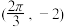 .
.(1)当
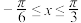 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值;
的值;(2)将函数
 的图象向右平移
的图象向右平移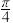 个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数 的图象,若
的图象,若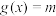 在
在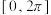 有两个不同的解,求实数
有两个不同的解,求实数 的取值范围.
的取值范围.
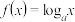 (
( ,且
,且 ),且
),且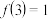 .
.(1)求
 的值,并写出函数
的值,并写出函数 的定义域;
的定义域;(2)设函数
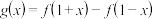 ,试判断
,试判断 的奇偶性,并说明理由;
的奇偶性,并说明理由;(3)若不等式
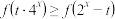 对任意
对任意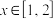 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
试卷分析
导出试卷题型(共 22题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 并集的概念及运算 解不含参数的一元二次不等式 | |
| 2 | 0.85 | 函数对称性的应用 | |
| 3 | 0.85 | 根据古典概型的概率求参数 | |
| 4 | 0.85 | 利用导数研究函数的零点 | |
| 5 | 0.65 | 函数奇偶性的应用 函数图像的识别 用导数判断或证明已知函数的单调性 | |
| 6 | 0.94 | 描述正(余)弦型函数图象的变换过程 | |
| 7 | 0.85 | 比较指数幂的大小 比较对数式的大小 | |
| 8 | 0.65 | 系统抽样 | |
| 二、多选题 | |||
| 9 | 0.65 | 由正弦(型)函数的值域(最值)求参数 求正弦(型)函数的对称轴及对称中心 相位变换及解析式特征 求sinx型三角函数的单调性 | |
| 10 | 0.4 | 函数极值的辨析 利用导数研究函数的零点 利用导数研究方程的根 利用导数研究函数图象及性质 | |
| 11 | 0.65 | 空间中的点(线)共面问题 求异面直线所成的角 判断线面平行 判断面面是否垂直 | |
| 12 | 0.65 | 根据交集结果求集合或参数 | |
| 三、填空题 | |||
| 13 | 0.85 | 根据交集结果求集合或参数 | 单空题 |
| 14 | 0.94 | 对数型函数图象过定点问题 | 单空题 |
| 15 | 0.65 | 等差数列的简单应用 | 单空题 |
| 16 | 0.85 | 由双曲线的离心率求参数的取值范围 根据a,b,c齐次式关系求渐近线方程 | 单空题 |
| 四、解答题 | |||
| 17 | 0.85 | 求sinx的函数的单调性 由正弦(型)函数的值域(最值)求参数 | 问答题 |
| 18 | 0.65 | 空间位置关系的向量证明 线面角的向量求法 面面角的向量求法 | 证明题 |
| 19 | 0.15 | 利用导数求函数的单调区间(不含参) 利用导数研究不等式恒成立问题 | 问答题 |
| 20 | 0.65 | 独立性检验解决实际问题 二项分布的均值 | 问答题 |
| 21 | 0.65 | 求含sinx(型)函数的值域和最值 求图象变化前(后)的解析式 | 问答题 |
| 22 | 0.65 | 利用函数单调性求最值或值域 函数奇偶性的定义与判断 对数函数单调性的应用 函数不等式恒成立问题 | 问答题 |

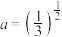 ,
,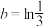 ,
,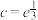 ,则(
,则(