江苏省无锡市江阴市普通高中2022-2023学年高三上学期期末数学试题
江苏
高三
期末
2023-01-24
1148次
整体难度:
适中
考查范围:
集合与常用逻辑用语、复数、空间向量与立体几何、函数与导数、数列、平面解析几何、三角函数与解三角形、等式与不等式、计数原理与概率统计、竞赛知识点、平面向量
一、单选题 添加题型下试题
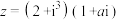 为纯虚数,则
为纯虚数,则 ( )
( )| A.0 | B. | C.2 | D.5 |
【知识点】 求复数的模解读 复数代数形式的乘法运算解读
A. 是 是 的充分不必要条件 的充分不必要条件 |
B.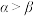 是 是 的必要不充分条件 的必要不充分条件 |
C. 是函数 是函数 为奇函数的充要条件 为奇函数的充要条件 |
D. 是函数 是函数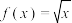 在 在 上单调递增的既不充分也不必要条件 上单调递增的既不充分也不必要条件 |
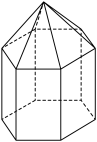
A.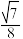 | B.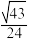 | C.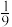 | D. |
【知识点】 棱柱表面积的有关计算 棱锥表面积的有关计算
 项和、前
项和、前 项和、前
项和、前 项和分别为
项和分别为 、
、 、
、 ,则下列等式正确的是( )
,则下列等式正确的是( )A.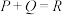 | B.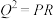 |
C. | D. |
【知识点】 等比数列子数列性质及应用 等比数列的其他性质
 中,若满足
中,若满足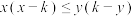 的点
的点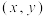 都在以坐标原点为圆心,2为半径的圆及其内部,则实数k的取值范围是( )
都在以坐标原点为圆心,2为半径的圆及其内部,则实数k的取值范围是( )A.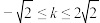 | B.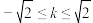 |
C.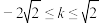 | D. |
【知识点】 由圆的位置关系确定参数或范围
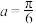 ,
,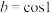 ,
, ,这三个数的大小关系为( )
,这三个数的大小关系为( )A.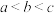 | B.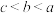 | C. | D. |
二、多选题 添加题型下试题
 与分针
与分针 长度分别为
长度分别为 和
和 ,设
,设 点为
点为 时刻,
时刻, 的面积为
的面积为 ,时间t(单位:时),则以下说法中正确的选项是( )
,时间t(单位:时),则以下说法中正确的选项是( )A.时针 旋转的角速度为 旋转的角速度为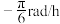 |
B.分针 旋转的角速度为 旋转的角速度为 |
C.一小时内(即 时), 时), 为锐角的时长是 为锐角的时长是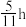 |
D.一昼夜内(即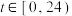 时), 时), 取得最大值为44次 取得最大值为44次 |
【知识点】 任意角的概念解读 求含sinx(型)函数的值域和最值解读
 ,
, 和
和 表示由甲箱取出的球是红球,白球和黑球的事件;再从乙箱中随机取出一球,以B表示由乙箱取出的球是红球的事件,则下列结论正确的是( )
表示由甲箱取出的球是红球,白球和黑球的事件;再从乙箱中随机取出一球,以B表示由乙箱取出的球是红球的事件,则下列结论正确的是( )A.事件B与事件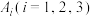 相互独立 相互独立 | B.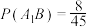 |
C.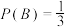 | D.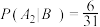 |
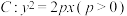 上的动点,
上的动点,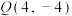 在抛物线C上,过抛物线C的焦点F的直线
在抛物线C上,过抛物线C的焦点F的直线 与抛物线C交于A,B两点,
与抛物线C交于A,B两点, ,
,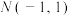 ,则( )
,则( )A. 的最小值为5 的最小值为5 |
B.若线段AB的中点为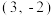 .则△NAB的面积为 .则△NAB的面积为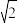 |
C.若 ,则直线的斜率为2 ,则直线的斜率为2 |
D.过点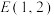 作两条直线与抛物线C分别交于点G,H,满足直线GH的斜率为 作两条直线与抛物线C分别交于点G,H,满足直线GH的斜率为 ,则EF平分 ,则EF平分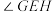 |
三、填空题 添加题型下试题
 中,直线
中,直线 与双曲线
与双曲线 的一条渐近线平行,且双曲线的一个焦点在直线l上,则双曲线的方程为
的一条渐近线平行,且双曲线的一个焦点在直线l上,则双曲线的方程为【知识点】 根据a、b、c求双曲线的标准方程
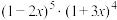 的展开式中,按
的展开式中,按 的升幂排列的第3项为
的升幂排列的第3项为【知识点】 求指定项的系数解读 两个二项式乘积展开式的系数问题解读
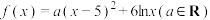 ,曲线
,曲线 在点
在点 处的切线与
处的切线与 轴相交于点
轴相交于点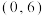 ,则函数
,则函数 的极小值为
的极小值为【知识点】 已知切线(斜率)求参数 求已知函数的极值
 ,向量
,向量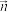 与向量
与向量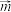 的夹角为
的夹角为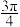 ,
, ,则向量
,则向量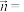
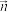 与向量
与向量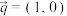 的夹角为
的夹角为 ,向量
,向量 ,其中
,其中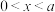 ,当
,当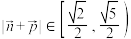 时,实数a的取值范围为
时,实数a的取值范围为四、解答题 添加题型下试题
 的前n项和为
的前n项和为 ,且
,且 ,
,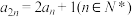 .
.(1)求数列
 的通项公式;
的通项公式;(2)若
 ,令
,令 ,求数列
,求数列 的前n项和
的前n项和 .
.
【知识点】 等差数列前n项和的基本量计算 错位相减法求和
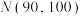 ,航天员在此项指标中的要求为
,航天员在此项指标中的要求为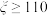 . 某学校共有2000名学生.为了宣传这一航天盛事,特意在本校举办了航天员的模拟选拔活动.学生首先要进行上述指标的筛查,对于符合要求的学生再进行4个环节选拔,且仅在通过一个环节后,才能进行到下一个环节的选拔.假设学生通过每个环节的概率均为
. 某学校共有2000名学生.为了宣传这一航天盛事,特意在本校举办了航天员的模拟选拔活动.学生首先要进行上述指标的筛查,对于符合要求的学生再进行4个环节选拔,且仅在通过一个环节后,才能进行到下一个环节的选拔.假设学生通过每个环节的概率均为 ,且相互独立.
,且相互独立.参考数据:
 ,
,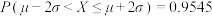 ,
,(1)设学生甲通过筛查后在后续的4个环节中参与的环节数量为X,请计算X的分布列与数学期望;
(2)请估计符合该项指标的学生人数(四舍五入结果取整数).以该人数为参加航天员选拔活动的名额,请计算最终通过学校选拔的人数Y的期望值.
 中,设曲线
中,设曲线 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,曲线
,曲线 上的点到原点O的最短距离为
上的点到原点O的最短距离为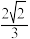 .以曲线
.以曲线 与坐标轴的交点为顶点的椭圆记为
与坐标轴的交点为顶点的椭圆记为 .
.(1)求椭圆
 的标准方程:
的标准方程:(2)设AB是过椭圆
 中心O的任意弦,l是线段AB的垂直平分线,M是l上的点(与O不重合),若M是l与椭圆
中心O的任意弦,l是线段AB的垂直平分线,M是l上的点(与O不重合),若M是l与椭圆 的交点,求
的交点,求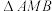 的面积的取值范围.
的面积的取值范围.
【知识点】 根据a、b、c求椭圆标准方程 椭圆中三角形(四边形)的面积
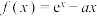 .
.(1)若
 有两个零点,求a的取值范围;
有两个零点,求a的取值范围;(2)若方程
 有两个实数根
有两个实数根 ,且
,且 ,证明:
,证明: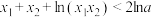 .
.
试卷分析
导出试卷题型(共 22题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 交并补混合运算 | |
| 2 | 0.94 | 求复数的模 复数代数形式的乘法运算 | |
| 3 | 0.85 | 判断命题的充分不必要条件 判断命题的必要不充分条件 充要条件的证明 | |
| 4 | 0.85 | 棱柱表面积的有关计算 棱锥表面积的有关计算 | |
| 5 | 0.65 | 函数图像的识别 指数函数图像应用 | |
| 6 | 0.4 | 等比数列子数列性质及应用 等比数列的其他性质 | |
| 7 | 0.65 | 由圆的位置关系确定参数或范围 | |
| 8 | 0.15 | 用导数判断或证明已知函数的单调性 比较正弦值的大小 比较余弦值的大小 | |
| 二、多选题 | |||
| 9 | 0.85 | 条件等式求最值 | |
| 10 | 0.65 | 任意角的概念 求含sinx(型)函数的值域和最值 | |
| 11 | 0.85 | 计算条件概率 条件概率性质的应用 条件概率 | |
| 12 | 0.65 | 求直线与抛物线相交所得弦的弦长 直线与抛物线相交求直线方程 直线与抛物线交点相关问题 根据韦达定理求参数 | |
| 三、填空题 | |||
| 13 | 0.65 | 根据a、b、c求双曲线的标准方程 | 单空题 |
| 14 | 0.85 | 求指定项的系数 两个二项式乘积展开式的系数问题 | 单空题 |
| 15 | 0.65 | 已知切线(斜率)求参数 求已知函数的极值 | 单空题 |
| 16 | 0.65 | 由cosx(型)函数的值域(最值)求参数 三角恒等变换的化简问题 坐标计算向量的模 向量夹角的坐标表示 | 双空题 |
| 四、解答题 | |||
| 17 | 0.65 | 正弦定理解三角形 余弦定理解三角形 | 问答题 |
| 18 | 0.65 | 等差数列前n项和的基本量计算 错位相减法求和 | 问答题 |
| 19 | 0.65 | 写出简单离散型随机变量分布列 求离散型随机变量的均值 二项分布的均值 指定区间的概率 | 问答题 |
| 20 | 0.85 | 证明线面垂直 证明面面垂直 面面角的向量求法 | 证明题 |
| 21 | 0.65 | 根据a、b、c求椭圆标准方程 椭圆中三角形(四边形)的面积 | 问答题 |
| 22 | 0.15 | 利用导数求函数的单调区间(不含参) 函数单调性、极值与最值的综合应用 利用导数证明不等式 利用导数研究函数的零点 | 证明题 |

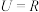 ,集合
,集合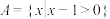 ,
,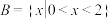 ,则
,则 (
(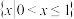
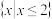

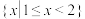
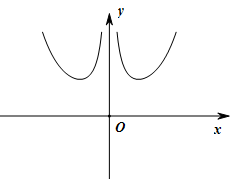
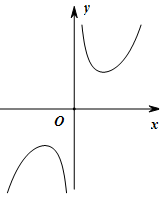
 的图象大致为(
的图象大致为(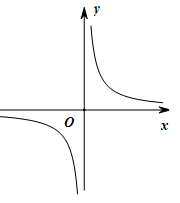
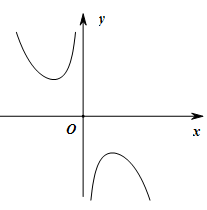
 ,
,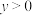 ,且
,且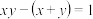 ,则下列结论正确的是(
,则下列结论正确的是(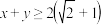
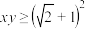
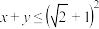
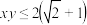
 中,AD是∠BAC的平分线,且交BC于D.
中,AD是∠BAC的平分线,且交BC于D. ;
;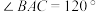 ,
, ,
,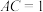 ,求BD.
,求BD.
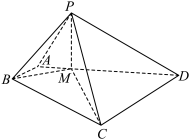
 中,
中, ,
, ,
,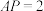 ,
,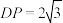 ,
,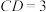 ,
,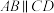 ,
, 平面PAD,点M满足
平面PAD,点M满足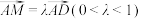 .
.
 ,求证:平面
,求证:平面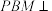 平面
平面 ;
; ,若
,若 ,求
,求 的值.
的值.


