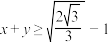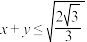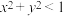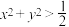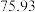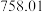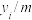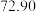浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
浙江
高三
三模
2023-03-17
3636次
整体难度:
适中
考查范围:
集合与常用逻辑用语、等式与不等式、复数、计数原理与概率统计、平面解析几何、函数与导数、空间向量与立体几何、平面向量、三角函数与解三角形、数列
浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
浙江
高三
三模
2023-03-17
3636次
整体难度:
适中
考查范围:
集合与常用逻辑用语、等式与不等式、复数、计数原理与概率统计、平面解析几何、函数与导数、空间向量与立体几何、平面向量、三角函数与解三角形、数列
一、单选题 添加题型下试题
单选题
|
较易(0.85)
名校
解题方法
您最近一年使用:0次
2023-03-16更新
|
847次组卷
|
3卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
单选题
|
较易(0.85)
名校
2. 若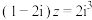 ,则
,则 ( )
( )
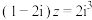 ,则
,则 ( )
( )A.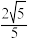 | B. | C. | D.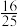 |
您最近一年使用:0次
2023-03-16更新
|
904次组卷
|
3卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
单选题
|
较易(0.85)
3.  的展开式中常数项为( )
的展开式中常数项为( )
 的展开式中常数项为( )
的展开式中常数项为( )| A.280 | B. | C.160 | D.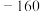 |
您最近一年使用:0次
2023-03-16更新
|
1386次组卷
|
3卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题(已下线)押新高考第4题 排列组合与二项式定理山东省淄博市四校(淄博市实验、齐盛中学、淄博十一中、淄博五中)高二下学期第一次模块考试数学试题
单选题
|
较难(0.4)
名校
解题方法
4. “省刻度尺”问题由英国数学游戏大师杜登尼提出:一根 长的尺子,要能够量出长度为
长的尺子,要能够量出长度为 到
到 且边长为整数的物体,至少需要6个刻度(尺子头尾不用刻).现有一根
且边长为整数的物体,至少需要6个刻度(尺子头尾不用刻).现有一根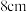 的尺子,要能够一次量出长度为
的尺子,要能够一次量出长度为 到
到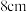 且边长为整数的物体,尺子上至少需要有( )个刻度
且边长为整数的物体,尺子上至少需要有( )个刻度
 长的尺子,要能够量出长度为
长的尺子,要能够量出长度为 到
到 且边长为整数的物体,至少需要6个刻度(尺子头尾不用刻).现有一根
且边长为整数的物体,至少需要6个刻度(尺子头尾不用刻).现有一根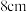 的尺子,要能够一次量出长度为
的尺子,要能够一次量出长度为 到
到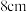 且边长为整数的物体,尺子上至少需要有( )个刻度
且边长为整数的物体,尺子上至少需要有( )个刻度| A.3 | B.4 | C.5 | D.6 |
【知识点】 实际问题中的组合计数问题解读
您最近一年使用:0次
2023-03-16更新
|
1756次组卷
|
7卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题(已下线)专题9-3 排列组合19种归类(理)(讲+练)-4北京市第二中学2023届高三校模数学试题(已下线)第六章 计数原理(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)专题01 两个计数原理与排列组合(7类压轴题型)-【常考压轴题】2023-2024学年高二数学压轴题攻略(人教A版2019选择性必修第三册)(已下线)思想04 运用转化与化归的思想方法解题(4大核心考点)(讲义)(已下线)【练】 专题一 排列数、组合数的性质应用问题(压轴大全)
单选题
|
较易(0.85)
5. 班级举行知识竞猜闯关活动,设置了 三个问题.答题者可自行决定答三题顺序.甲有
三个问题.答题者可自行决定答三题顺序.甲有 的可能答对问题
的可能答对问题 ,
,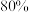 的可能答对问题
的可能答对问题 ,
, 的可能答对问题
的可能答对问题 .记答题者连续答对两题的概率为
.记答题者连续答对两题的概率为 ,要使得
,要使得 最大,他应该先回答( )
最大,他应该先回答( )
 三个问题.答题者可自行决定答三题顺序.甲有
三个问题.答题者可自行决定答三题顺序.甲有 的可能答对问题
的可能答对问题 ,
,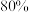 的可能答对问题
的可能答对问题 ,
, 的可能答对问题
的可能答对问题 .记答题者连续答对两题的概率为
.记答题者连续答对两题的概率为 ,要使得
,要使得 最大,他应该先回答( )
最大,他应该先回答( )A.问题 | B.问题 | C.问题 和 和 都可以 都可以 | D.问题 |
您最近一年使用:0次
2023-03-16更新
|
1035次组卷
|
4卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
单选题
|
适中(0.65)
解题方法
6. 在平面直角坐标系上,圆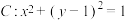 ,直线
,直线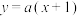 与圆
与圆 交于
交于 两点,
两点, ,则当
,则当 的面积最大时,
的面积最大时, ( )
( )
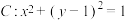 ,直线
,直线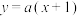 与圆
与圆 交于
交于 两点,
两点, ,则当
,则当 的面积最大时,
的面积最大时, ( )
( )A. | B.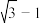 | C. | D. |
【知识点】 由标准方程确定圆心和半径 圆的弦长与中点弦 圆内接三角形的面积
您最近一年使用:0次
单选题
|
适中(0.65)
名校
7. 设 ,
,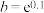 ,
,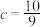 ,则( )
,则( )
 ,
,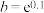 ,
,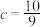 ,则( )
,则( )A.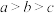 | B.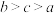 | C.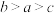 | D. |
【知识点】 用导数判断或证明已知函数的单调性 比较函数值的大小关系
您最近一年使用:0次
2023-03-16更新
|
933次组卷
|
4卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
单选题
|
困难(0.15)
名校
解题方法
8. 在正方体 中,平面
中,平面 经过点B、D,平面
经过点B、D,平面 经过点A、
经过点A、 ,当平面
,当平面 分别截正方体所得截面面积最大时,平面
分别截正方体所得截面面积最大时,平面 所成的锐二面角大小为( )
所成的锐二面角大小为( )
 中,平面
中,平面 经过点B、D,平面
经过点B、D,平面 经过点A、
经过点A、 ,当平面
,当平面 分别截正方体所得截面面积最大时,平面
分别截正方体所得截面面积最大时,平面 所成的锐二面角大小为( )
所成的锐二面角大小为( )A. | B. | C. | D.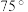 |
【知识点】 由导数求函数的最值(不含参) 求二面角
您最近一年使用:0次
2023-03-16更新
|
1961次组卷
|
6卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题(已下线)专题8 立体几何初步(2)(已下线)专题突破卷20立体几何的截面问题-2陕西省咸阳市实验中学2022-2023学年高一下学期第二次月考数学试题(已下线)第6章 空间向量与立体几何 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第二章 立体几何中的计算 专题一 空间角 微点10 二面角大小的计算综合训练【培优版】
二、多选题 添加题型下试题
多选题
|
适中(0.65)
名校
9. 在平面直角坐标系中,已知点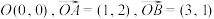 ,则( )
,则( )
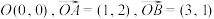 ,则( )
,则( )A.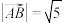 |
B. 是直角三角形 是直角三角形 |
C. 在 在 方向上的投影向量的坐标为 方向上的投影向量的坐标为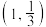 |
D.与 垂直的单位向量的坐标为 垂直的单位向量的坐标为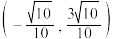 或 或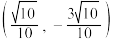 |
您最近一年使用:0次
2023-03-16更新
|
1730次组卷
|
6卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
多选题
|
较难(0.4)
10. 已知函数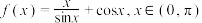 ,则( )
,则( )
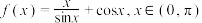 ,则( )
,则( )A. 有一个零点 有一个零点 | B. 在 在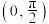 上单调递减 上单调递减 |
C. 有两个极值点 有两个极值点 | D.若 ,则 ,则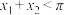 |
您最近一年使用:0次
11. 设椭圆 ,
,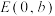 ,
,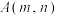 为椭圆
为椭圆 上一点,
上一点,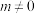 ,点
,点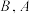 关于
关于 轴对称,直线
轴对称,直线 分别与
分别与 轴交于
轴交于 两点,则( )
两点,则( )
 ,
,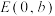 ,
,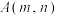 为椭圆
为椭圆 上一点,
上一点,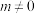 ,点
,点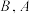 关于
关于 轴对称,直线
轴对称,直线 分别与
分别与 轴交于
轴交于 两点,则( )
两点,则( )A.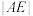 的最大值为 的最大值为 |
B.直线 的斜率乘积为定值 的斜率乘积为定值 |
C.若 轴上存在点 轴上存在点 ,使得 ,使得 ,则 ,则 的坐标为 的坐标为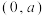 或 或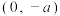 |
D.直线 过定点 过定点 |
您最近一年使用:0次
三、填空题 添加题型下试题
填空题-单空题
|
容易(0.94)
名校
解题方法
13. 已知随机变量 服从正态分布
服从正态分布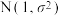 ,若
,若 ,则
,则
_____________ .
 服从正态分布
服从正态分布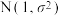 ,若
,若 ,则
,则
【知识点】 根据正态曲线的对称性求参数
您最近一年使用:0次
2023-03-16更新
|
949次组卷
|
3卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
填空题-单空题
|
较易(0.85)
名校
14. 写出一个满足下列条件的正弦型函数,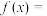
____________ .
①最小正周期为 ; ②
; ② 在
在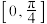 上单调递增; ③
上单调递增; ③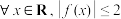 成立.
成立.
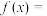
①最小正周期为
 ; ②
; ② 在
在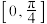 上单调递增; ③
上单调递增; ③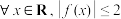 成立.
成立.
您最近一年使用:0次
2023-03-16更新
|
869次组卷
|
3卷引用:浙江省金丽衢十二校、“七彩阳光”2023届高三下学期3月联考数学试题
填空题-单空题
|
适中(0.65)
解题方法
15. 将两个形状完全相同的正三棱锥底面重合得到一个六面体,若六面体存在外接球,且正三棱锥的体积为1,则六面体外接球的体积为_____________ .
【知识点】 球的体积的有关计算 多面体与球体内切外接问题
您最近一年使用:0次
填空题-单空题
|
较难(0.4)
16. 已知椭圆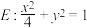 ,椭圆的左右焦点分别为
,椭圆的左右焦点分别为 ,点
,点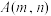 为椭圆上一点且
为椭圆上一点且 ,过A作椭圆E的切线l,并分别交
,过A作椭圆E的切线l,并分别交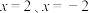 于C、D点.连接
于C、D点.连接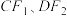 ,
,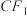 与
与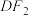 交于点E,并连接
交于点E,并连接 .若直线l,
.若直线l, 的斜率之和为
的斜率之和为 ,则点A坐标为
,则点A坐标为_____________ .
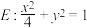 ,椭圆的左右焦点分别为
,椭圆的左右焦点分别为 ,点
,点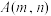 为椭圆上一点且
为椭圆上一点且 ,过A作椭圆E的切线l,并分别交
,过A作椭圆E的切线l,并分别交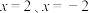 于C、D点.连接
于C、D点.连接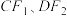 ,
,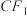 与
与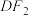 交于点E,并连接
交于点E,并连接 .若直线l,
.若直线l, 的斜率之和为
的斜率之和为 ,则点A坐标为
,则点A坐标为【知识点】 求椭圆的切线方程 根据直线与椭圆的位置关系求参数或范围
您最近一年使用:0次
四、解答题 添加题型下试题
17. 已知数列 是以d为公差的等差数列,
是以d为公差的等差数列, 为
为 的前n项和.
的前n项和.
(1)若 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若 中的部分项组成的数列
中的部分项组成的数列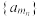 是以
是以 为首项,4为公比的等比数列,且
为首项,4为公比的等比数列,且 ,求数列
,求数列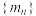 的前n项和
的前n项和 .
.
 是以d为公差的等差数列,
是以d为公差的等差数列, 为
为 的前n项和.
的前n项和.(1)若
 ,求数列
,求数列 的通项公式;
的通项公式;(2)若
 中的部分项组成的数列
中的部分项组成的数列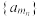 是以
是以 为首项,4为公比的等比数列,且
为首项,4为公比的等比数列,且 ,求数列
,求数列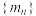 的前n项和
的前n项和 .
.
您最近一年使用:0次
解答题-问答题
|
适中(0.65)
解题方法
18. 已知 中角A,B,C对应的边分别是a,b,c,已知
中角A,B,C对应的边分别是a,b,c,已知 .
.
(1)证明: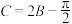 ;
;
(2)求 的面积.
的面积.
 中角A,B,C对应的边分别是a,b,c,已知
中角A,B,C对应的边分别是a,b,c,已知 .
.(1)证明:
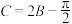 ;
;(2)求
 的面积.
的面积.
您最近一年使用:0次
解答题-问答题
|
适中(0.65)
19. 如图,四面体 中,
中,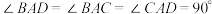 ,
, ,
, 与面
与面 的所成角为
的所成角为 .
.
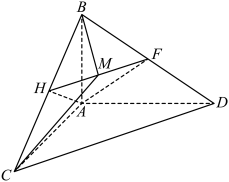
(1)若四面体 的体积为
的体积为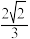 ,求
,求 的长;
的长;
(2)设点 在面
在面 中,
中,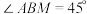 ,
,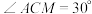 ,过
,过 作
作 的平行线,分别交
的平行线,分别交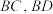 于点
于点 ,求面
,求面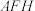 与面
与面 所成夹角的余弦值.
所成夹角的余弦值.
 中,
中,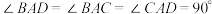 ,
, ,
, 与面
与面 的所成角为
的所成角为 .
.
(1)若四面体
 的体积为
的体积为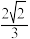 ,求
,求 的长;
的长;(2)设点
 在面
在面 中,
中,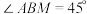 ,
,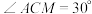 ,过
,过 作
作 的平行线,分别交
的平行线,分别交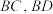 于点
于点 ,求面
,求面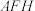 与面
与面 所成夹角的余弦值.
所成夹角的余弦值.
【知识点】 锥体体积的有关计算 求二面角 面面角的向量求法 由线面角的大小求长度
您最近一年使用:0次
解答题-问答题
|
适中(0.65)
解题方法
20. 大坝是一座具有灌溉、防洪、发电、航运、养殖和游览等综合效益的大型水利枢纽工程.为预测渗压值和控制库水位,工程师在水库选取一支编号为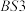 的渗压计,随机收集
的渗压计,随机收集 个该渗压计管内水位和水库水位监测数据:
个该渗压计管内水位和水库水位监测数据:
并计算得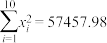 ,
,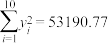 ,
,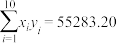 .
.
(1)估计该水库中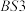 号渗压计管内平均水位与水库的平均水位;
号渗压计管内平均水位与水库的平均水位;
(2)求该水库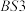 号渗压计管内水位与水库水位的样本相关系数(精确到
号渗压计管内水位与水库水位的样本相关系数(精确到 );
);
(3)某天雨后工程师测量了水库水位,并得到水库的水位为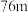 .利用以上数据给出此时
.利用以上数据给出此时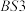 号渗压计管内水位的估计值.
号渗压计管内水位的估计值.
附:相关系数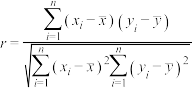 ,
,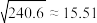 ,
,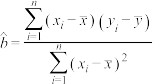 ,
,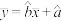 .
.
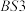 的渗压计,随机收集
的渗压计,随机收集 个该渗压计管内水位和水库水位监测数据:
个该渗压计管内水位和水库水位监测数据:样本号 |
|
|
|
|
|
|
|
|
|
| 总和 |
水库水位 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
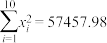 ,
,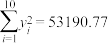 ,
,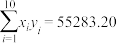 .
.(1)估计该水库中
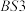 号渗压计管内平均水位与水库的平均水位;
号渗压计管内平均水位与水库的平均水位;(2)求该水库
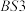 号渗压计管内水位与水库水位的样本相关系数(精确到
号渗压计管内水位与水库水位的样本相关系数(精确到 );
);(3)某天雨后工程师测量了水库水位,并得到水库的水位为
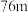 .利用以上数据给出此时
.利用以上数据给出此时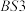 号渗压计管内水位的估计值.
号渗压计管内水位的估计值.附:相关系数
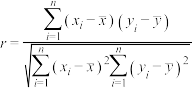 ,
,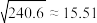 ,
,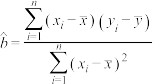 ,
,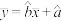 .
.
您最近一年使用:0次
解答题-问答题
|
较难(0.4)
解题方法
21. 设双曲线 的右焦点为
的右焦点为 ,右焦点到双曲线的渐近线的距离为
,右焦点到双曲线的渐近线的距离为 .
.
(1)求双曲线 的方程;
的方程;
(2)若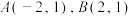 ,点
,点 在线段
在线段 上(不含端点),过点
上(不含端点),过点 分别作双曲线两支的切线,切点分别为
分别作双曲线两支的切线,切点分别为 .连接
.连接 ,并过
,并过 的中点
的中点 分别作双曲线两支的切线,切点分别为
分别作双曲线两支的切线,切点分别为 ,求
,求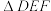 面积的最小值.
面积的最小值.
 的右焦点为
的右焦点为 ,右焦点到双曲线的渐近线的距离为
,右焦点到双曲线的渐近线的距离为 .
.(1)求双曲线
 的方程;
的方程;(2)若
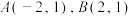 ,点
,点 在线段
在线段 上(不含端点),过点
上(不含端点),过点 分别作双曲线两支的切线,切点分别为
分别作双曲线两支的切线,切点分别为 .连接
.连接 ,并过
,并过 的中点
的中点 分别作双曲线两支的切线,切点分别为
分别作双曲线两支的切线,切点分别为 ,求
,求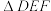 面积的最小值.
面积的最小值.
您最近一年使用:0次
解答题-问答题
|
困难(0.15)
解题方法
22. 已知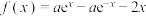
(1)当 时,求
时,求 单调区间;
单调区间;
(2)当 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)设 ,
, ,证明:
,证明: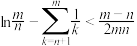 .
.
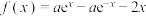
(1)当
 时,求
时,求 单调区间;
单调区间;(2)当
 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;(3)设
 ,
, ,证明:
,证明: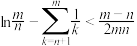 .
.
您最近一年使用:0次
试卷分析
导出
整体难度:适中
考查范围:集合与常用逻辑用语、等式与不等式、复数、计数原理与概率统计、平面解析几何、函数与导数、空间向量与立体几何、平面向量、三角函数与解三角形、数列
试卷题型(共 22题)
题型
数量
单选题
8
多选题
4
填空题
4
解答题
6
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.85 | 交集的概念及运算 分式不等式 根式不等式 | |
| 2 | 0.85 | 复数代数形式的乘法运算 复数的除法运算 共轭复数的概念及计算 | |
| 3 | 0.85 | 求二项展开式的第k项 两个二项式乘积展开式的系数问题 | |
| 4 | 0.4 | 实际问题中的组合计数问题 | |
| 5 | 0.85 | 独立事件的乘法公式 | |
| 6 | 0.65 | 由标准方程确定圆心和半径 圆的弦长与中点弦 圆内接三角形的面积 | |
| 7 | 0.65 | 用导数判断或证明已知函数的单调性 比较函数值的大小关系 | |
| 8 | 0.15 | 由导数求函数的最值(不含参) 求二面角 | |
| 二、多选题 | |||
| 9 | 0.65 | 零向量与单位向量 坐标计算向量的模 向量垂直的坐标表示 求投影向量 | |
| 10 | 0.4 | 用导数判断或证明已知函数的单调性 利用导数证明不等式 利用导数研究函数的零点 求已知函数的极值点 | |
| 11 | 0.4 | 求椭圆中的弦长 椭圆中的直线过定点问题 椭圆中存在定点满足某条件问题 椭圆中的定值问题 | |
| 12 | 0.4 | 利用导数证明不等式 基本不等式求和的最小值 | |
| 三、填空题 | |||
| 13 | 0.94 | 根据正态曲线的对称性求参数 | 单空题 |
| 14 | 0.85 | 利用正弦型函数的单调性求参数 由正弦(型)函数的周期性求值 | 单空题 |
| 15 | 0.65 | 球的体积的有关计算 多面体与球体内切外接问题 | 单空题 |
| 16 | 0.4 | 求椭圆的切线方程 根据直线与椭圆的位置关系求参数或范围 | 单空题 |
| 四、解答题 | |||
| 17 | 0.65 | 由递推关系式求通项公式 求递推关系式 等差数列通项公式的基本量计算 分组(并项)法求和 | 问答题 |
| 18 | 0.65 | 用导数判断或证明已知函数的单调性 二倍角的余弦公式 正弦定理边角互化的应用 三角形面积公式及其应用 | 问答题 |
| 19 | 0.65 | 锥体体积的有关计算 求二面角 面面角的向量求法 由线面角的大小求长度 | 问答题 |
| 20 | 0.65 | 计算几个数的平均数 用回归直线方程对总体进行估计 求回归直线方程 相关系数的计算 | 问答题 |
| 21 | 0.4 | 根据a、b、c求双曲线的标准方程 根据直线与双曲线的位置关系求参数或范围 求双曲线中三角形(四边形)的面积问题 | 问答题 |
| 22 | 0.15 | 利用导数求函数的单调区间(不含参) 利用导数证明不等式 利用导数研究不等式恒成立问题 | 问答题 |

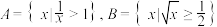 ,则
,则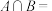 (
(
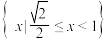
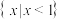

 ,且
,且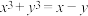 ,则(
,则(