专题07 立体几何中的向量方法
【要点提炼】
1.直线与平面、平面与平面的平行与垂直的向量方法
设直线l的方向向量为a=(a1,b1,c1),平面α,β的法向量分别为μ=(a2,b2,c2),v=(a3,b3,c3),则
(1)线面平行
l∥α⇔a⊥μ⇔a·μ=0⇔a1a2+b1b2+c1c2=0.
(2)线面垂直
l⊥α⇔a∥μ⇔a=kμ⇔a1=ka2,b1=kb2,c1=kc2.
(3)面面平行
α∥β⇔μ∥v⇔μ=λv⇔a2=λa3,b2=λb3,c2=λc3.
(4)面面垂直
α⊥β⇔μ⊥v⇔μ·v=0⇔a2a3+b2b3+c2c3=0.
2.直线与直线、直线与平面、平面与平面的夹角计算
设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2),平面α,β的法向量分别为μ=(a3,b3,c3),v=(a4,b4,c4)(以下相同).
(1)线线夹角
设l,m的夹角为θ![]() ,则cos θ=
,则cos θ=![]() =
=![]() .
.
(2)线面夹角
设直线l与平面α的夹角为θ![]() ,则sin θ=|cosa,μ|=
,则sin θ=|cosa,μ|=![]() .
.
(3)面面夹角
设平面α,β的夹角为θ(0≤θ<π),则|cos θ|=|cosμ,v|=![]() .
.
考点
考向一 利用空间向量证明平行、垂直
【典例1】 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
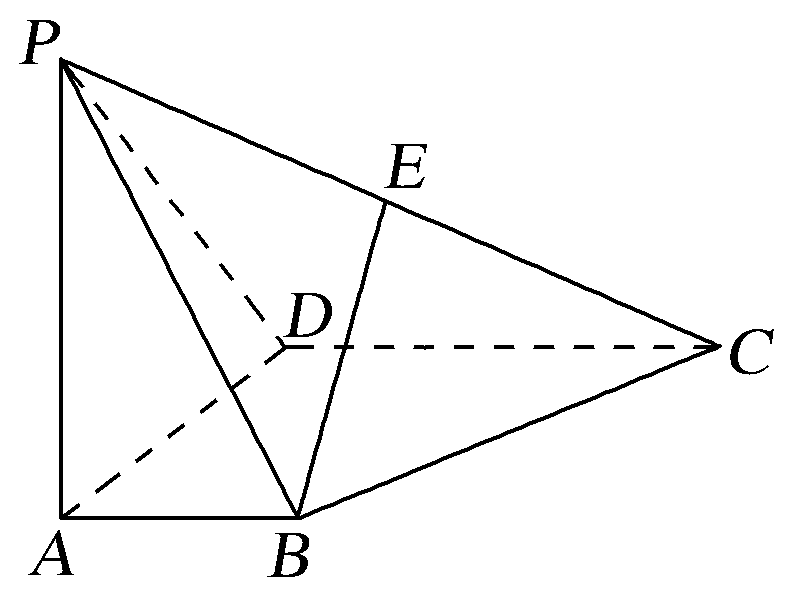
(1)BE⊥DC;
(2)BE∥平面PAD;
(3)平面PCD⊥平面PAD.
证明 依题意,以点A为原点建立空间直角坐标系(如图),可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).由E为棱PC的中点,得E(1,1,1).
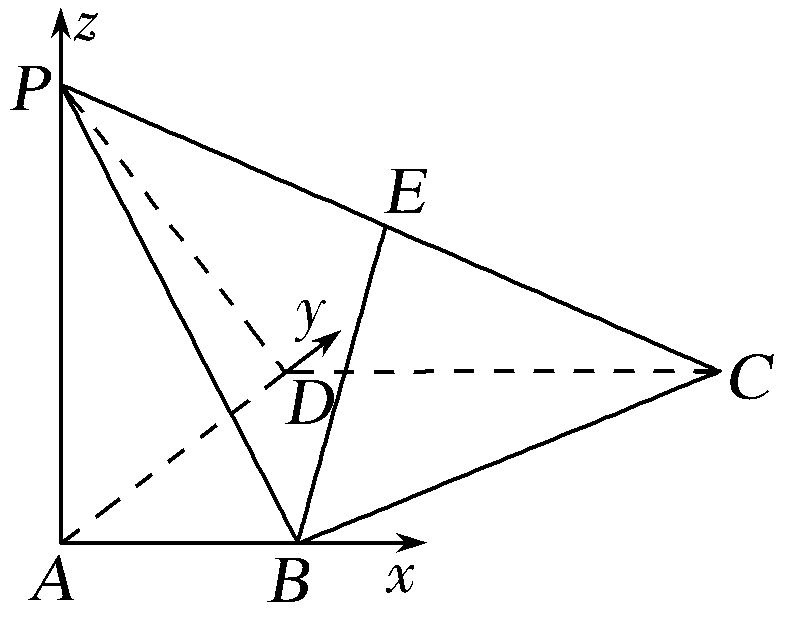
(1)向量![]() =(0,1,1),
=(0,1,1),![]() =(2,0,0),故
=(2,0,0),故![]() ·
·![]() =0.
=0.
所以BE⊥DC.
(2)因为AB⊥AD,又PA⊥平面ABCD,AB⊂平面ABCD,
所以AB⊥PA,PA∩AD=A,PA,AD⊂平面PAD,
所以AB⊥平面PAD,
所以向量![]() =(1,0,0)为平面PAD的一个法向量,
=(1,0,0)为平面PAD的一个法向量,
而![]() ·
·![]() =(0,1,1)·(1,0,0)=0,所以BE⊥AB,
=(0,1,1)·(1,0,0)=0,所以BE⊥AB,
又BE⊄平面PAD,
所以BE∥平面PAD.
(3)由(2)知平面PAD的法向量![]() =(1,0,0),向量
=(1,0,0),向量![]() =(0,2,-2),
=(0,2,-2),![]() =(2,0,0),
=(2,0,0),
设平面PCD的法向量为n=(x,y,z),
则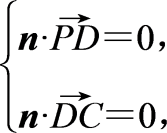 即
即![]()
不妨令y=1,可得n=(0,1,1)为平面PCD的一个法向量.
且n·![]() =(0,1,1)·(1,0,0)=0,所以n⊥
=(0,1,1)·(1,0,0)=0,所以n⊥![]() .
.
所以平面PAD⊥平面PCD.
探究提高 1.利用向量法证明平行、垂直,关键是建立恰当的坐标系(尽可能利用垂直条件,准确写出相关点的坐标,进而用向量表示涉及到直线、平面的要素).
2.向量证明的核心是利用向量的数量积或数乘向量,但向量证明仍然离不开立体几何的定理,如在(2)中忽略BE⊄平面PAD而致误.
【拓展练习1】
(1)OM∥平面BCF;
(2)平面MDF⊥平面EFCD.
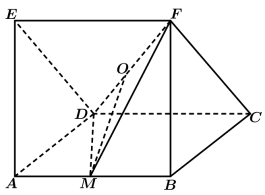
【知识点】 空间位置关系的向量证明
考向二 线线角、线面角的求解
【典例2】 (2020·浙江卷)如图,在三棱台ABC-DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.
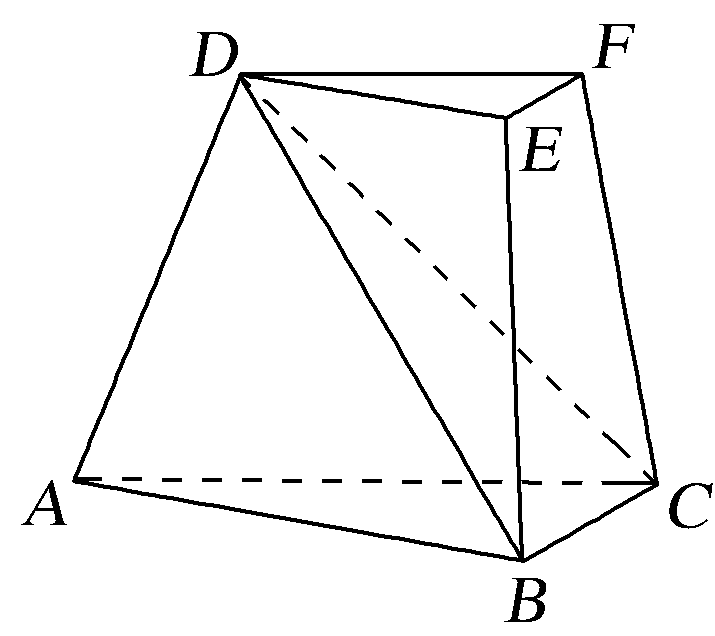
(1)证明:EF⊥DB;
(2)求直线DF与平面DBC所成角的正弦值.
(1)证明 如图(1),过点D作DO⊥AC,交直线AC于点O,连接OB.
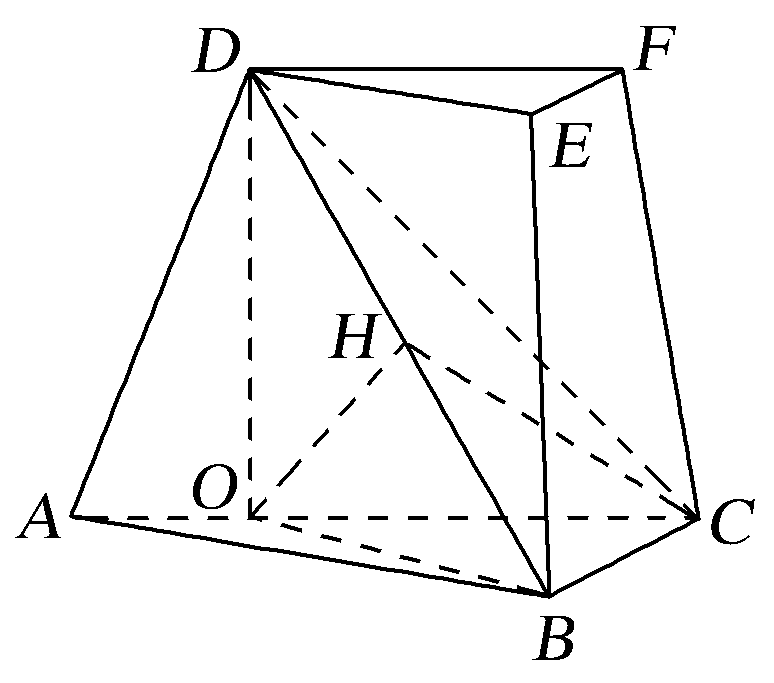
图(1)
由∠ACD=45°,DO⊥AC,得
CD=![]() CO.
CO.
由平面ACFD⊥平面ABC,得DO⊥平面ABC,
所以DO⊥BC.
由∠ACB=45°,
BC=![]() CD=
CD=![]() CO,得BO⊥BC.
CO,得BO⊥BC.
所以BC⊥平面BDO,故BC⊥DB.
由ABC-DEF为三棱台,得BC∥EF,所以EF⊥DB.
(2)解 法一 如图(1),过点O作OH⊥BD,交直线BD于点H,连接CH.由ABC-DEF为三棱台,得DF∥CO,所以直线DF与平面DBC所成角等于直线CO与平面DBC所成角.
由BC⊥平面BDO,得OH⊥BC,故OH⊥平面DBC,
所以∠OCH为直线CO与平面DBC所成角.
设CD=2![]() ,
,
则DO=OC=2,BO=BC=![]() ,得BD=
,得BD=![]() ,OH=
,OH=![]()
![]() ,所以sin∠OCH=
,所以sin∠OCH=![]() =
=![]() .
.
因此,直线DF与平面DBC所成角的正弦值为![]() .
.
法二 由ABC-DEF为三棱台,得DF∥CO,所以直线DF与平面DBC所成角等于直线CO与平面DBC所成角,记为θ.
如图(2),以O为原点,分别以射线OC,OD为y,z轴的正半轴,建立空间直角坐标系O-xyz.
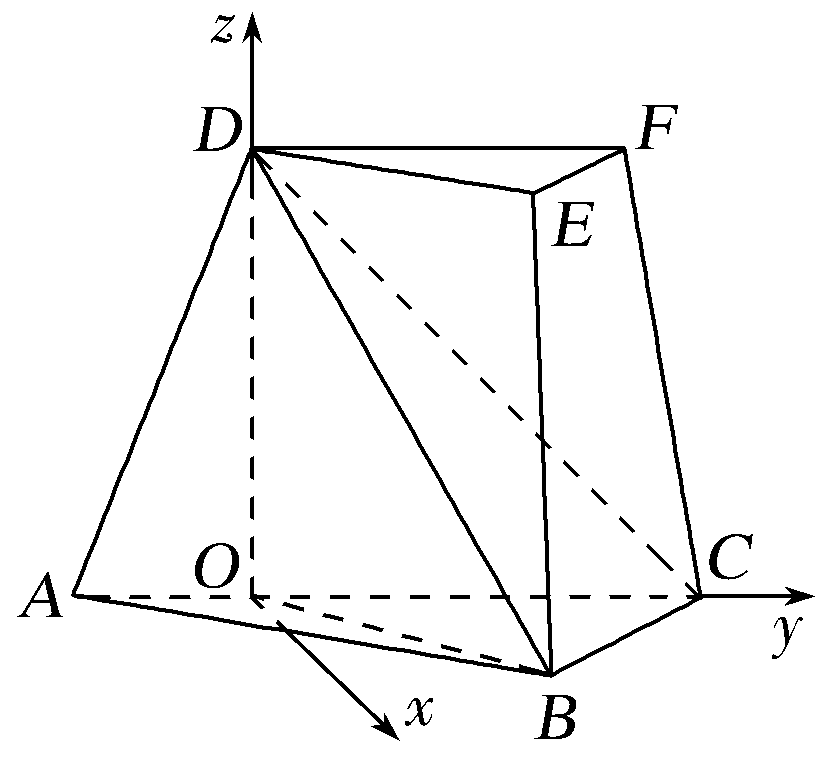
图(2)
设CD=2![]() ,
,
由题意知各点坐标如下:
O(0,0,0),B(1,1,0),C(0,2,0),D(0,0,2).
因此![]() =(0,2,0),
=(0,2,0),![]() =(-1,1,0),
=(-1,1,0),![]() =(0,-2,2).
=(0,-2,2).
设平面DBC的一个法向量为n=(x,y,z),
由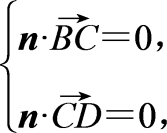 即
即![]() 可取n=(1,1,1),
可取n=(1,1,1),
所以sin θ=|cos〈![]() ,n〉|=
,n〉|=![]() =
=![]() .
.
因此,直线DF与平面DBC所成角的正弦值为![]() .
.
探究提高 1.异面直线所成的角θ,可以通过两直线的方向向量的夹角φ求得,即cos θ=|cos φ|.
2.直线与平面所成的角θ主要通过直线的方向向量与平面的法向量的夹角φ求得,即sin θ=|cos φ|,有时也可分别求出斜线与它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角).
【拓展练习2】 (2020·全国Ⅱ卷)
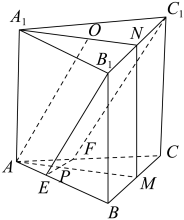
(2)设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.
考向三 利用向量求二面角
【典例3】 (2020·全国Ⅲ卷)如图,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1.
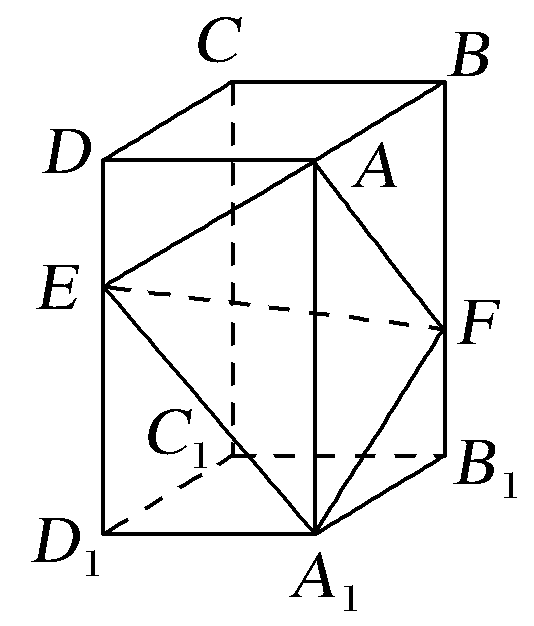
(1)证明:点C1在平面AEF内;
(2)若AB=2,AD=1,AA1=3,求二面角A-EF-A1的正弦值.
解 设AB=a,AD=b,AA1=c.如图,以C1为坐标原点,![]() 的方向为x轴正方向, 建立空间直角坐标系C1-xyz.
的方向为x轴正方向, 建立空间直角坐标系C1-xyz.
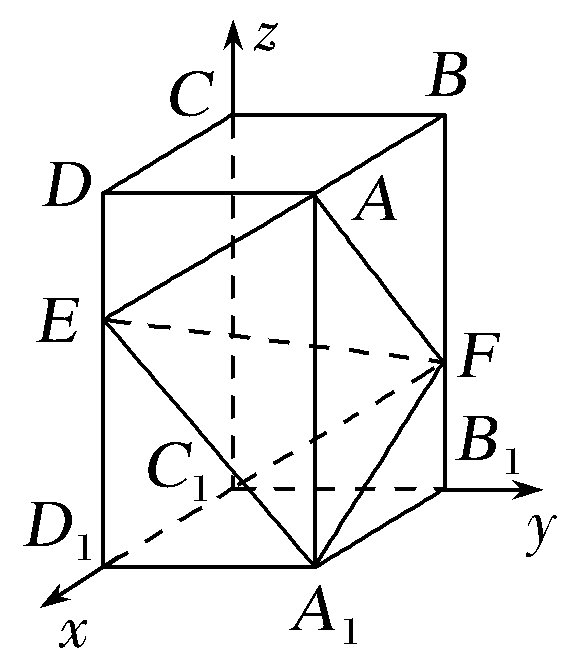
(1)证明 连接C1F,C1(0,0,0),A(a,b,c),E![]() ,F
,F![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,得
,得![]() =
=![]() ,
,
因此EA∥C1F,即A,E,F,C1四点共面,
所以点C1在平面AEF内.
(2)由已知得A(2,1,3),E(2,0,2),F(0,1,1),A1(2,1,0),![]() =(0,-1,-1),
=(0,-1,-1),![]() =(-2,0,-2),
=(-2,0,-2),![]() =(0,-1,2),
=(0,-1,2),![]() =(-2,0,1).
=(-2,0,1).
设n1=(x,y,z)为平面AEF的法向量,则
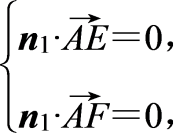 即
即![]() 可取n1=(-1,-1,1).
可取n1=(-1,-1,1).
设n2为平面A1EF的法向量,则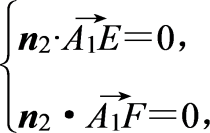
同理可取n2=![]() .
.
设二面角A-EF-A1的平面角为α,所以cos α=cos〈n1,n2〉=![]() =-
=-![]() ,
,
则sin α=![]() =
=![]() ,
,
所以二面角A-EF-A1的正弦值为![]() .
.
探究提高 1.二面角的大小可以利用分别在两个半平面内与棱垂直的直线的方向向量的夹角(或其补角)或通过二面角的两个面的法向量的夹角求得,它等于两个法向量的夹角或其补角.
2.利用向量法求二面角,必须能判定“所求二面角的平面角是锐角或钝角”,否则解法是不严谨的.
【拓展练习3】 (2020·沈阳一监)
 为等边三角形,
为等边三角形, 为等腰直角三角形,
为等腰直角三角形,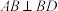 ,平面
,平面 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且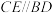 ,
,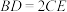 .点F为AD中点,连接EF.
.点F为AD中点,连接EF.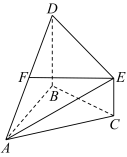
(1)求证:
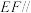 平面ABC;
平面ABC;(2)求二面角
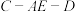 的余弦值.
的余弦值.
考向四 利用空间向量求解探索性问题
【典例4】 (2020·武汉调研)如图所示,在正方体ABCD-A1B1C1D1中,点O是AC与BD的交点,点E是线段OD1上的一点.
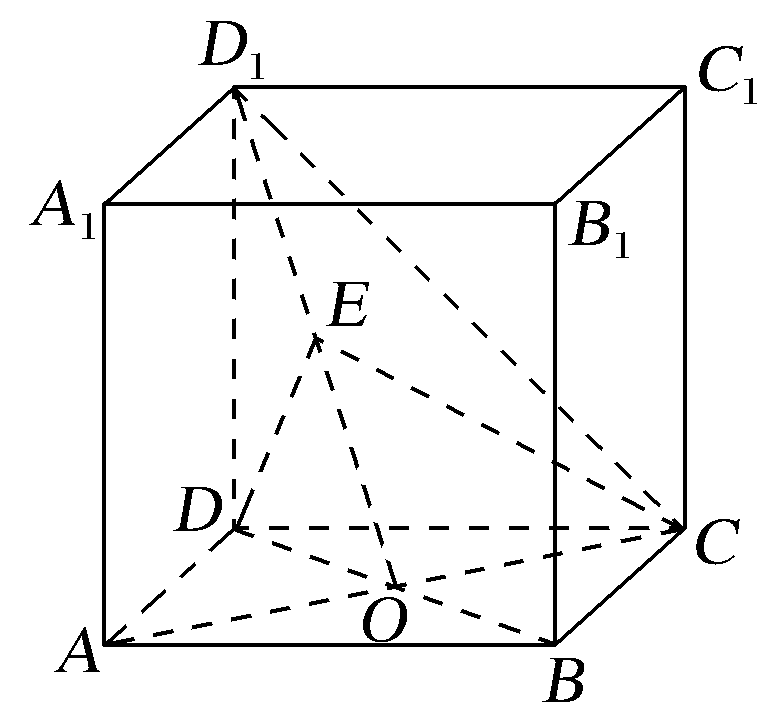
(1)若点E为OD1的中点,求直线OD1与平面CDE所成角的正弦值;
(2)是否存在点E,使得平面CDE⊥平面CD1O?若存在,请指出点E的位置,并加以证明;若不存在,请说明理由.
解 (1)不妨设正方体的棱长为2.
以D为坐标原点,分别以DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系D-xyz,
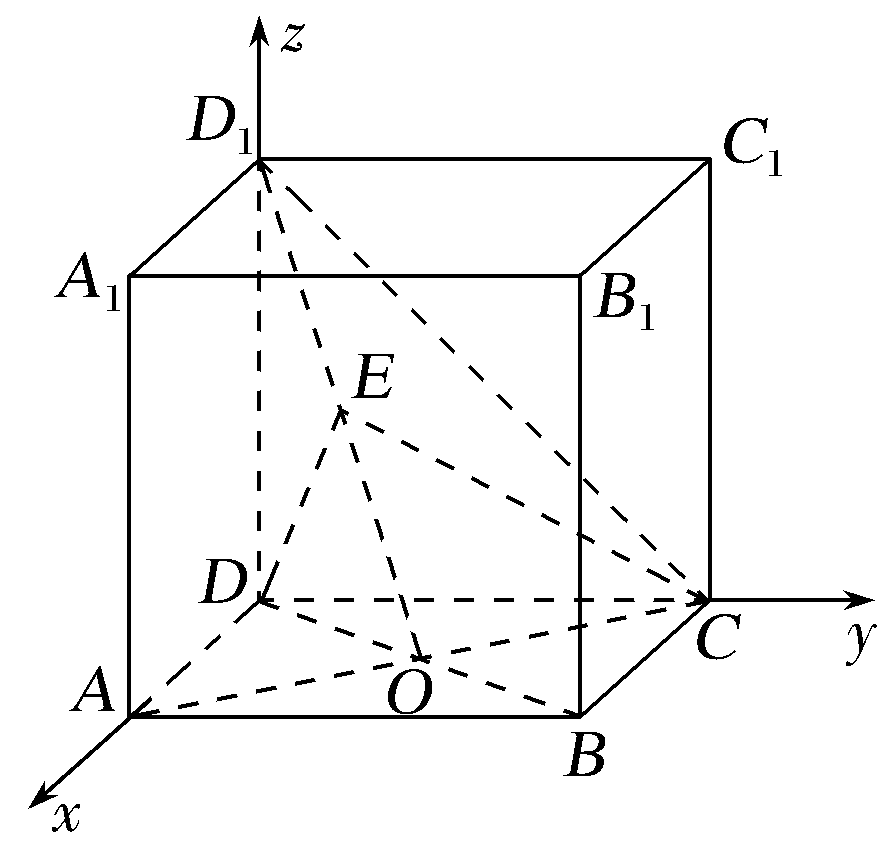
则D(0,0,0),D1(0,0,2),C(0,2,0),O(1,1,0).
因为E为OD1的中点,
所以E![]() .
.
则![]() =(-1,-1,2),
=(-1,-1,2),![]() =
=![]() ,
,![]() =(0,2,0).
=(0,2,0).
设p=(x0,y0,z0)是平面CDE的法向量,
则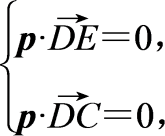 即
即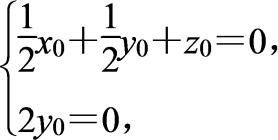
取x0=2,则y0=0,z0=-1,
所以p=(2,0,-1)为平面CDE的一个法向量.
设直线OD1与平面CDE所成角为θ,
所以sin θ=|cos〈![]() ,p〉|=
,p〉|=![]()
=![]() =
=![]() ,
,
即直线OD1与平面CDE所成角的正弦值为![]() .
.
(2)存在,且点E为线段OD1上靠近点O的三等分点.理由如下.
假设存在点E,使得平面CDE⊥平面CD1O.
同第(1)问建立空间直角坐标系,易知点E不与点O重合,
设![]() =λ
=λ![]() ,λ∈[0,+∞),
,λ∈[0,+∞),![]() =(-1,1,0),
=(-1,1,0),![]() =(-1,-1,2).
=(-1,-1,2).
设m=(x1,y1,z1)是平面CD1O的法向量,
则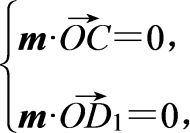 即
即![]()
取x1=1,则y1=1,z1=1,
所以m=(1,1,1)为平面CD1O的一个法向量.
因为![]() =λ
=λ![]() ,所以点E的坐标为
,所以点E的坐标为![]() ,
,
所以![]() =
=![]() .
.
设n=(x2,y2,z2)是平面CDE的法向量,
则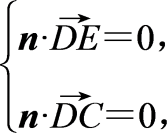 即
即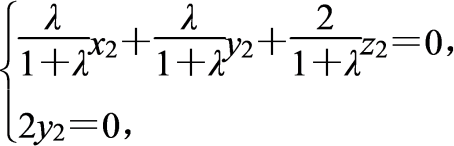
取x2=1,则y2=0,z2=-![]() ,
,
所以n=![]() 为平面CDE的一个法向量.
为平面CDE的一个法向量.
因为平面CDE⊥平面CD1O,所以m⊥n.
则m·n=0,所以1-![]() =0,解得λ=2.
=0,解得λ=2.
所以当![]() =2,即点E为线段OD1上靠近点O的三等分点时,平面CDE⊥平面CD1O.
=2,即点E为线段OD1上靠近点O的三等分点时,平面CDE⊥平面CD1O.
探究提高 1.空间向量最适合于解决立体几何中的探索性问题,它无需进行复杂的作图、论证、推理,只需通过坐标运算进行判断.但注意空间坐标系建立的规范性及计算的准确性,否则容易出现错误.
2.空间向量求解探索性问题:(1)假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论;(2)在这个前提下进行逻辑推理,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标(或参数)是否有解,是否有规定范围内的解”等.若由此推导出矛盾,则否定假设;否则,给出肯定结论.
【拓展练习4】 (2019·北京卷)
 .
.(Ⅰ)求证:CD⊥平面PAD;
(Ⅱ)求二面角F–AE–P的余弦值;
(Ⅲ)设点G在PB上,且
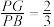 .判断直线AG是否在平面AEF内,说明理由.
.判断直线AG是否在平面AEF内,说明理由.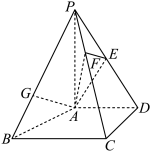
【知识点】 证明线面垂直 空间位置关系的向量证明 面面角的向量求法
【专题拓展练习】
一、单选题
 中,
中, 分别为
分别为 的中点,点
的中点,点 在正方体的表面上运动,且满足
在正方体的表面上运动,且满足 ,则下列说法正确的是( )
,则下列说法正确的是( )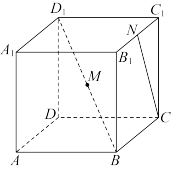
A.点 可以是棱 可以是棱 的中点 的中点 | B.线段 的最大值为 的最大值为 |
C.点 的轨迹是正方形 的轨迹是正方形 | D.点 轨迹的长度为 轨迹的长度为 |
【知识点】 空间位置关系的向量证明 立体几何中的轨迹问题
 中,底面ABCD为矩形,
中,底面ABCD为矩形, 底面
底面 ,
, ,E为PC的中点,则异面直线PD与BE所成角的余弦值为( )
,E为PC的中点,则异面直线PD与BE所成角的余弦值为( )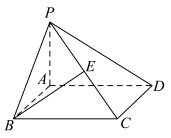
A. | B. | C. | D.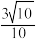 |
 底面是边长为
底面是边长为 的正方形,
的正方形,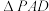 是以
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 平面
平面 ,点
,点 是线段
是线段 上的动点(不含端点),若线
上的动点(不含端点),若线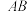 段上存在点
段上存在点 (不含端点),使得异面直线
(不含端点),使得异面直线 与
与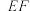 成
成 的角,则线段
的角,则线段 长的取值范围是( )
长的取值范围是( )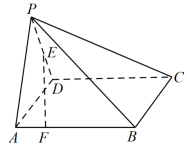
A.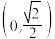 | B.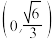 | C. | D.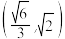 |
【知识点】 已知线线角求其他量
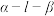 ,其中平面的一个法向量
,其中平面的一个法向量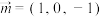 ,平面
,平面 的一个法向量
的一个法向量 ,则二面角
,则二面角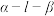 的大小可能为( )
的大小可能为( )A. | B. | C. 或 或 | D. |
【知识点】 面面角的向量求法
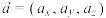 ,
,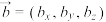 ,
, 是空间中的一个单位正交基底.规定向量积的行列式计算:
是空间中的一个单位正交基底.规定向量积的行列式计算: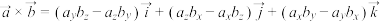
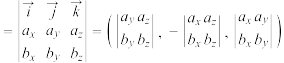 ,其中行列式计算表示为
,其中行列式计算表示为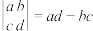 ,若向量
,若向量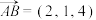 ,
,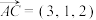 ,则
,则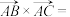 ( )
( )A.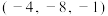 | B.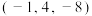 | C.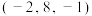 | D.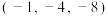 |
【知识点】 空间向量的坐标表示
 ,
,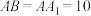 ,
, ,
, 在左侧面
在左侧面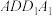 上,已知
上,已知 到
到 、
、 的距离均为5,则过点
的距离均为5,则过点 且与
且与 垂直的长方体截面的形状为( )
垂直的长方体截面的形状为( )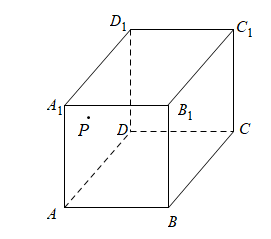
| A.六边形 | B.五边形 |
| C.四边形 | D.三角形 |
【知识点】 判断正方体的截面形状 空间位置关系的向量证明
 的棱长为1,点E是底面ABCD上的动点,则
的棱长为1,点E是底面ABCD上的动点,则 的最大值为( )
的最大值为( )A. | B.1 | C. | D. |
【知识点】 求空间向量的数量积 空间向量数量积的应用
 .若点M为PD中点,则直线CM与PB所成角的大小为( )
.若点M为PD中点,则直线CM与PB所成角的大小为( )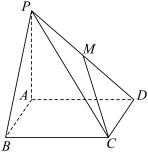
| A.60° | B.45° | C.30° | D.90° |
【知识点】 异面直线夹角的向量求法
 中,
中, ,记平面
,记平面 与平面
与平面 、平面
、平面 、平面
、平面 ,所成的锐二面角分别为
,所成的锐二面角分别为 、
、 、
、 ,则( )
,则( )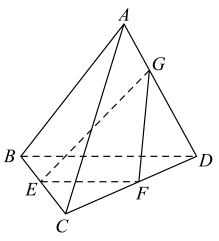
A. | B.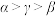 | C.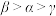 | D. |
【知识点】 面面角的向量求法
 的棱长为
的棱长为 ,
, 、
、 、
、 分别为
分别为 、
、 、
、 的中点,则( )
的中点,则( )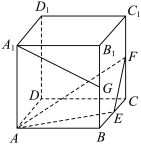
A.直线 与直线 与直线 垂直 垂直 |
B.直线 与平面 与平面 平行 平行 |
C.平面 截正方体所得的截面面积为 截正方体所得的截面面积为 |
D.点 和点 和点 到平面 到平面 的距离相等 的距离相等 |
【知识点】 空间位置关系的向量证明 点到平面距离的向量求法
 是棱长为
是棱长为 的正方体,
的正方体, 、
、 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且 .当
.当 、
、 、
、 、
、 共面时,平面
共面时,平面 与平面
与平面 所成锐二面角的余弦值为( )
所成锐二面角的余弦值为( )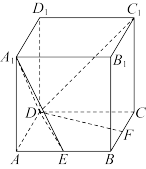
A. | B. | C. | D. |
【知识点】 面面角的向量求法
二、解答题
 ,将矩形ABCD折起,使点A与点C重合,折痕为EF,连接AF、CE,以AF和EF为折痕,将四边形ABFE折起,使点B落在线段FC上,将
,将矩形ABCD折起,使点A与点C重合,折痕为EF,连接AF、CE,以AF和EF为折痕,将四边形ABFE折起,使点B落在线段FC上,将 向上折起,使平面DEC⊥平面FEC,如图2.
向上折起,使平面DEC⊥平面FEC,如图2.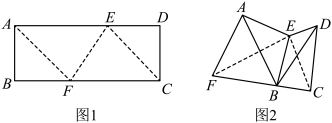
(1)证明:平面ABE⊥平面EFC;
(2)连接BE、BD,求锐二面角A-BE-D的正弦值.


 ,用
,用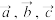 表示
表示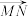 ,则
,则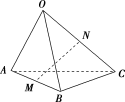
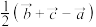
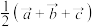
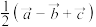
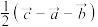
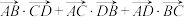 =(
=( ,
,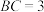 ,
,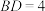 ,若
,若 与
与 互余,则
互余,则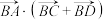 的最大值为(
的最大值为(



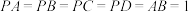 ,点
,点 ,
, 分别在棱
分别在棱 上运动,当
上运动,当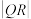 达到最小值时,
达到最小值时,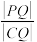 的值为(
的值为(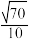
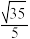
 中,
中, ,
,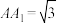 ,
, ,
,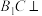 平面
平面 ,
, 的中点.
的中点.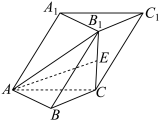
 平面
平面 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
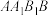 ,
,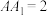 ,
,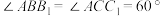 ,
, 为
为
 平面
平面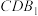 ;
;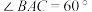 ,求直线
,求直线 与平面
与平面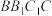 所成角的正弦值.
所成角的正弦值.
 都是正方形,平面
都是正方形,平面 平面
平面 分别为
分别为 的中点.
的中点.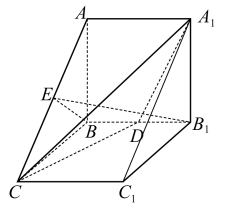
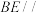 平面
平面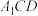 .
.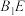 与平面
与平面

