河北省2023届高三上学期省级联测数学试题
河北
高三
模拟预测
2022-12-02
4212次
整体难度:
容易
考查范围:
集合与常用逻辑用语、等式与不等式、函数与导数、复数、数列、三角函数与解三角形、平面解析几何、平面向量、空间向量与立体几何、计数原理与概率统计
一、单选题 添加题型下试题
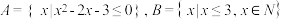 ,则
,则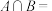 ( )
( )A.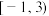 | B.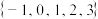 | C.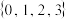 | D. |
【知识点】 交集的概念及运算解读 解不含参数的一元二次不等式解读
 若
若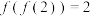 ,则
,则 ( )
( )| A.0 | B. | C. | D.1 |
【知识点】 已知分段函数的值求参数或自变量解读 对数的运算
 ,则复数
,则复数 可能为( )
可能为( )A. | B. | C. | D.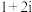 |
 的前
的前 项和为
项和为 ,若
,若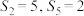 ,则
,则 ( )
( )| A.7 | B.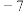 | C.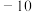 | D.10 |
【知识点】 等差数列前n项和的基本量计算
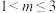 ,则
,则 的取值范围为( )
的取值范围为( )A. | B.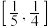 | C.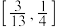 | D.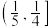 |
 (
( ,
, )上存在
)上存在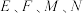 四点,使得四边形
四点,使得四边形 为正方形,且原点
为正方形,且原点 为正方形中心,
为正方形中心,  为双曲线右顶点,
为双曲线右顶点, 在第一象限,
在第一象限, ,设双曲线的离心率为
,设双曲线的离心率为 ,则
,则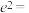 ( )
( )A.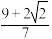 | B. | C.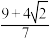 | D.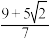 |
【知识点】 求双曲线的离心率或离心率的取值范围
二、多选题 添加题型下试题
A.若 ,则 ,则 |
B.三个数 成等比数列的充要条件是 成等比数列的充要条件是 |
C.向量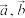 共线的充要条件是有且仅有一个实数 共线的充要条件是有且仅有一个实数 ,使 ,使 |
D.已知命题 时, 时,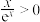 ,则命题 ,则命题 的否定为: 的否定为: 时, 时,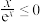 |
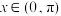 时,
时, ,并且满足
,并且满足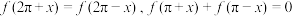 ,则下列关于函数
,则下列关于函数 说法正确的是( )
说法正确的是( )A.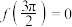 | B.周期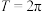 |
C. 的图象关于 的图象关于 对称 对称 | D. 的图象关于 的图象关于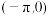 对称 对称 |
【知识点】 函数周期性的应用 判断证明抽象函数的周期性 函数对称性的应用
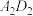 的中点,下列说法正确的是( )
的中点,下列说法正确的是( )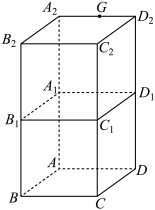
A.平面 平面 平面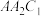 | B.三棱锥 的体积为 的体积为 |
C.该几何体外接球的体积为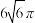 | D.若 为动点,且 为动点,且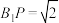 ,则 ,则 点运动轨迹与该几何体表面相交的长度为 点运动轨迹与该几何体表面相交的长度为 |
【知识点】 多面体与球体内切外接问题 判断面面是否垂直 立体几何中的轨迹问题
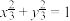 便是它的一种表达式,下列有关说法正确的是( )
便是它的一种表达式,下列有关说法正确的是( )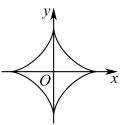
A.星形线关于 对称 对称 | B.星形线图象围成的面积小于2 |
C.星形线上的点到 轴,y轴距离乘积的最大值为 轴,y轴距离乘积的最大值为 | D.星形线上的点到原点距离的最小值为 |
【知识点】 求可行域的面积解读 基本不等式求积的最大值解读 由方程研究曲线的性质
三、填空题 添加题型下试题
【知识点】 分步乘法计数原理及简单应用解读 分组分配问题解读
 服从正态分布
服从正态分布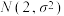 ,且
,且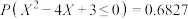 ,则
,则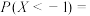
 ,则
,则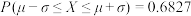 ,
,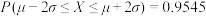 ,
,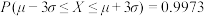 )
)
【知识点】 特殊区间的概率解读 根据正态曲线的对称性求参数
 为一条直径,
为一条直径, 为圆上两点且弦
为圆上两点且弦 长为
长为 ,则
,则 的取值范围是
的取值范围是【知识点】 数量积的坐标表示解读 坐标法的应用——直线与圆的位置关系
四、解答题 添加题型下试题
 中,
中, 是等腰直角三角形,
是等腰直角三角形, ,
,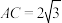 ,平面
,平面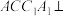 底面
底面 ,
,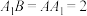 .
.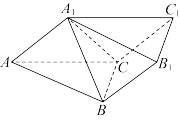
(1)证明:
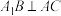 ;
;(2)求平面
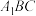 与平面
与平面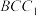 夹角的正弦值.
夹角的正弦值.
【知识点】 线面垂直证明线线垂直 面面垂直证线面垂直 面面角的向量求法
 ,椭圆上的点到两焦点的距离和为
,椭圆上的点到两焦点的距离和为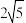 ,点
,点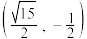 在椭圆
在椭圆 上.
上.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
 作直线
作直线 交椭圆于
交椭圆于 两点,点
两点,点 为点
为点 关于
关于 轴的对称点,求
轴的对称点,求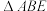 面积的最大值.
面积的最大值.
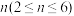 次结果相同则得
次结果相同则得 分(规定连续抛掷结果不同不得分,如正反正反正反不得分,正正反正反反得4分),小红每抛掷一次正面结果则得2分,得分高者获胜.
分(规定连续抛掷结果不同不得分,如正反正反正反不得分,正正反正反反得4分),小红每抛掷一次正面结果则得2分,得分高者获胜.(1)求小红得8分的概率;
(2)求小明得分的分布列和期望,并比较两人谁获胜的概率大?
 .
.(1)当
 时,求
时,求 的单调性;
的单调性;(2)若
 恒大于0,求
恒大于0,求 的取值范围.
的取值范围.
试卷分析
导出试卷题型(共 22题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 交集的概念及运算 解不含参数的一元二次不等式 | |
| 2 | 0.85 | 已知分段函数的值求参数或自变量 对数的运算 | |
| 3 | 0.94 | 复数的相等 求复数的实部与虚部 复数代数形式的乘法运算 共轭复数的概念及计算 | |
| 4 | 0.94 | 等差数列前n项和的基本量计算 | |
| 5 | 0.65 | 万能公式 二倍角的余弦公式 | |
| 6 | 0.85 | 复杂(根式型、分式型等)函数的值域 利用函数单调性求最值或值域 利用导数求函数的单调区间(不含参) 由导数求函数的最值(不含参) | |
| 7 | 0.85 | 作差法比较代数式的大小 | |
| 8 | 0.65 | 求双曲线的离心率或离心率的取值范围 | |
| 二、多选题 | |||
| 9 | 0.85 | 全称命题的否定及其真假判断 平面向量共线定理证明点共线问题 确定等比中项 由已知条件判断所给不等式是否正确 | |
| 10 | 0.65 | 函数周期性的应用 判断证明抽象函数的周期性 函数对称性的应用 | |
| 11 | 0.65 | 多面体与球体内切外接问题 判断面面是否垂直 立体几何中的轨迹问题 | |
| 12 | 0.65 | 求可行域的面积 基本不等式求积的最大值 由方程研究曲线的性质 | |
| 三、填空题 | |||
| 13 | 0.65 | 分步乘法计数原理及简单应用 分组分配问题 | 单空题 |
| 14 | 0.65 | 特殊区间的概率 根据正态曲线的对称性求参数 | 单空题 |
| 15 | 0.65 | 判断零点所在的区间 求已知函数的极值点 | 单空题 |
| 16 | 0.85 | 数量积的坐标表示 坐标法的应用——直线与圆的位置关系 | 单空题 |
| 四、解答题 | |||
| 17 | 0.85 | 二倍角的正弦公式 余弦定理解三角形 | 问答题 |
| 18 | 0.85 | 裂项相消法求和 累乘法求数列通项 | 问答题 |
| 19 | 0.65 | 线面垂直证明线线垂直 面面垂直证线面垂直 面面角的向量求法 | 证明题 |
| 20 | 0.65 | 根据a、b、c求椭圆标准方程 求椭圆中的最值问题 根据韦达定理求参数 复合函数的最值 | 问答题 |
| 21 | 0.65 | 计算古典概型问题的概率 写出简单离散型随机变量分布列 独立重复试验的概率问题 求离散型随机变量的均值 | 应用题 |
| 22 | 0.15 | 用导数判断或证明已知函数的单调性 利用导数研究不等式恒成立问题 | 问答题 |

 ,则
,则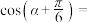 (
(

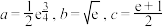 ,则(
,则(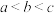
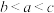
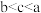
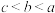
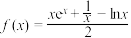 ,
, 是该函数的极值点,定义
是该函数的极值点,定义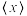 表示超过实数
表示超过实数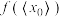 的值为
的值为 在
在 边上,
边上, 平分
平分 ,
,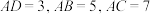 .
. ;
;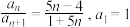 .
.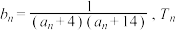 为
为 的前
的前 .
.


