广东省潮州市2023届高三模拟数学试题
广东
高三
模拟预测
2023-06-05
1019次
整体难度:
容易
考查范围:
集合与常用逻辑用语、等式与不等式、复数、三角函数与解三角形、数列、平面解析几何、空间向量与立体几何、计数原理与概率统计、函数与导数、平面向量
一、单选题 添加题型下试题
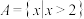 ,
,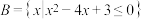 则
则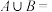 ( )
( )A.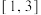 | B. | C. | D. |
【知识点】 并集的概念及运算解读 解不含参数的一元二次不等式解读
 为第二象限角,且
为第二象限角,且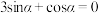 ,则
,则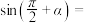 ( )
( )A. | B.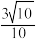 | C.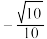 | D.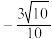 |
【知识点】 由条件等式求正、余弦解读 诱导公式五、六解读
 ,第2关收税金为剩余金的
,第2关收税金为剩余金的 ,第3关收税金为剩余金的
,第3关收税金为剩余金的 ,第4关收税金为剩余金的
,第4关收税金为剩余金的 ,第5关收税金为剩余金的
,第5关收税金为剩余金的 ,5关所收税金之和恰好重1斤.问原来持金多少?”.记这个人原来持金为
,5关所收税金之和恰好重1斤.问原来持金多少?”.记这个人原来持金为 斤,设
斤,设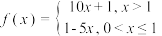 ,则
,则 ( )
( )A. | B.7 | C.13 | D.26 |
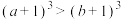 ”是“
”是“ ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
【知识点】 判断命题的必要不充分条件解读
 上一点
上一点 作圆
作圆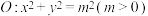 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,若
,若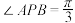 ,则实数
,则实数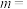 ( )
( )A. | B. | C. | D. |
【知识点】 已知切线求参数
 ,
, ,其中
,其中 ,且
,且 ,
,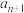 是方程
是方程 的实数根,则
的实数根,则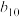 等于( )
等于( )| A.24 | B.32 | C.48 | D.64 |
【知识点】 根据数列递推公式写出数列的项
 的外接球的球心为
的外接球的球心为 ,
, 平面
平面 ,
, ,
,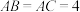 ,
, ,则球心O到平面
,则球心O到平面 的距离为( )
的距离为( )A. | B. | C. | D. |
【知识点】 多面体与球体内切外接问题 求点面距离
二、多选题 添加题型下试题
 ,则下列说法正确的是( )
,则下列说法正确的是( )A.焦点为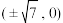 | B.渐近线方程为3x±4y=0 |
C.离心率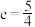 | D.焦点到渐近线的距离为4 |
【知识点】 求双曲线的焦点坐标 已知方程求双曲线的渐近线
 内,得分60分以下为不及格,其得分的频率分布直方图如图所示(按得分分成
内,得分60分以下为不及格,其得分的频率分布直方图如图所示(按得分分成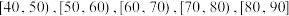 这五组),则下列结论正确的是( )
这五组),则下列结论正确的是( )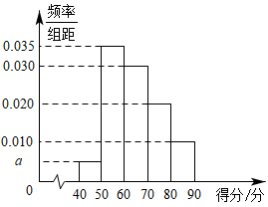
A.直方图中 |
| B.此次比赛得分不及格的共有40人 |
C.以频率为概率,从这100名参赛者中随机选取1人,其得分在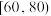 的概率为0.5 的概率为0.5 |
| D.这100名参赛者得分的中位数为65 |
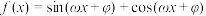
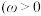 ,
,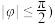 的最小正周期为
的最小正周期为 ,且过点
,且过点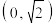 ,则下列正确的有( )
,则下列正确的有( )A. 在 在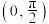 单调递减 单调递减 |
B. 的一条对称轴为 的一条对称轴为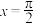 |
C.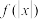 的周期为 的周期为 |
D.把函数 的图象向左平移 的图象向左平移 个长度单位得到函数 个长度单位得到函数 的解析式为 的解析式为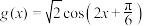 |
 在
在 上可导且
上可导且 ,其导函数
,其导函数 满足
满足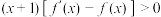 ,对于函数
,对于函数 ,下列结论正确的是( )
,下列结论正确的是( )A.函数 在 在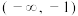 上为增函数 上为增函数 | B. 是函数 是函数 的极小值点 的极小值点 |
C.函数 必有2个零点 必有2个零点 | D.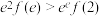 |
【知识点】 函数单调性、极值与最值的综合应用 利用导数研究函数的零点
三、填空题 添加题型下试题
 ,
, ,
, ,
, )组成的学习小组中选出4名进行观后体会交流,则男生
)组成的学习小组中选出4名进行观后体会交流,则男生 和女生甲没有被同时选中的概率为
和女生甲没有被同时选中的概率为【知识点】 实际问题中的组合计数问题解读 计算古典概型问题的概率
 ,其外接球的表面积为
,其外接球的表面积为 ,则
,则 的最小值为
的最小值为【知识点】 圆柱表面积的有关计算 球的表面积的有关计算
 :
: 的焦点为
的焦点为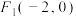 ,
,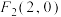 .过
.过 且倾斜角为60°的直线交椭圆的上半部分于点
且倾斜角为60°的直线交椭圆的上半部分于点 ,以
,以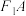 ,
,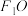 (
( 为坐标原点)为邻边作平行四边形
为坐标原点)为邻边作平行四边形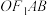 ,点
,点 恰好也在椭圆上,则
恰好也在椭圆上,则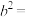
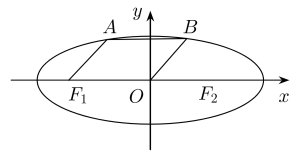
【知识点】 椭圆的对称性 根据椭圆过的点求标准方程
四、解答题 添加题型下试题
 的前
的前 项和为
项和为 ,且
,且 ,
,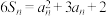 .
.(1)求数列
 的通项公式;
的通项公式;(2)若
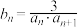 ,求数列
,求数列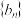 的前
的前 项和
项和 .
.
【知识点】 判断等差数列 裂项相消法求和 利用an与sn关系求通项或项
 中,角A,B,C的对边分别是a,b,c,已知
中,角A,B,C的对边分别是a,b,c,已知 ,
, .
.(1)求角B的大小;
(2)若
 的面积
的面积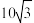 ,设D是BC的中点,求
,设D是BC的中点,求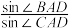 的值.
的值.
 左侧)掷冰壶一次.当所有成员全部掷完冰壶后,开始计分.若冰壶未到达营垒区,计
左侧)掷冰壶一次.当所有成员全部掷完冰壶后,开始计分.若冰壶未到达营垒区,计 分;若冰壶能准确到达营垒区,计2分,整场比赛累计得分多者获得比赛胜利.已知
分;若冰壶能准确到达营垒区,计2分,整场比赛累计得分多者获得比赛胜利.已知 队两名成员甲、乙每次将冰壶投掷到营垒区的概率分别为
队两名成员甲、乙每次将冰壶投掷到营垒区的概率分别为 和
和 ,
, 队两名成员丙、丁每次将冰壶投掷到营垒区的概率均为
队两名成员丙、丁每次将冰壶投掷到营垒区的概率均为 .假设两队投掷的冰壶在运动过程中无碰撞,每名成员投掷冰壶相互独立,每局比赛互不影响.
.假设两队投掷的冰壶在运动过程中无碰撞,每名成员投掷冰壶相互独立,每局比赛互不影响.
(1)求
 队每局得分
队每局得分 的分布列及期望;
的分布列及期望;(2)若第一局比赛结束后,
 队得1分,
队得1分, 队得4分,求
队得4分,求 队最终获得本场比赛胜利且总积分比
队最终获得本场比赛胜利且总积分比 队高3分的概率.
队高3分的概率.
 中,侧面
中,侧面 侧面
侧面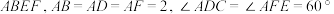 ,M为
,M为 上的动点.
上的动点.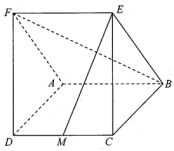
(1)当M为
 的中点时,证明:
的中点时,证明: ;
;(2)求
 与平面
与平面 所成角的正弦值的取值范围.
所成角的正弦值的取值范围.
【知识点】 证明线面垂直 线面垂直证明线线垂直 线面角的向量求法
 中,动圆M与圆
中,动圆M与圆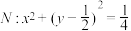 相内切,且与直线
相内切,且与直线 相切,记动圆圆心M的轨迹为曲线C.
相切,记动圆圆心M的轨迹为曲线C.(1)求曲线C的方程;
(2)过点
 的直线l与曲线C交于A,B两点,分别以A,B为切点作曲线C的切线
的直线l与曲线C交于A,B两点,分别以A,B为切点作曲线C的切线 ,直线
,直线 相交于点P.若
相交于点P.若 ,求直线l的方程.
,求直线l的方程.
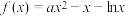 .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)若函数
 在定义域内有两个不相等的零点
在定义域内有两个不相等的零点 .
.①求实数a的取值范围;
②证明:
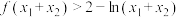 .
.
试卷分析
导出试卷题型(共 22题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.85 | 并集的概念及运算 解不含参数的一元二次不等式 | |
| 2 | 0.85 | 复数的坐标表示 复数的除法运算 共轭复数的概念及计算 | |
| 3 | 0.85 | 由条件等式求正、余弦 诱导公式五、六 | |
| 4 | 0.85 | 裂项相消法求和 数列-其他模型 | |
| 5 | 0.85 | 判断命题的必要不充分条件 | |
| 6 | 0.85 | 已知切线求参数 | |
| 7 | 0.85 | 根据数列递推公式写出数列的项 | |
| 8 | 0.4 | 多面体与球体内切外接问题 求点面距离 | |
| 二、多选题 | |||
| 9 | 0.85 | 求双曲线的焦点坐标 已知方程求双曲线的渐近线 | |
| 10 | 0.85 | 由频率分布直方图计算频率、频数、样本容量、总体容量 由频率分布直方图估计中位数 用频率估计概率 | |
| 11 | 0.65 | 求cosx型三角函数的单调性 由正(余)弦函数的性质确定图象(解析式) 求图象变化前(后)的解析式 辅助角公式 | |
| 12 | 0.65 | 函数单调性、极值与最值的综合应用 利用导数研究函数的零点 | |
| 三、填空题 | |||
| 13 | 0.65 | 向量夹角的计算 已知模求数量积 | 单空题 |
| 14 | 0.85 | 实际问题中的组合计数问题 计算古典概型问题的概率 | 单空题 |
| 15 | 0.85 | 圆柱表面积的有关计算 球的表面积的有关计算 | 单空题 |
| 16 | 0.85 | 椭圆的对称性 根据椭圆过的点求标准方程 | 单空题 |
| 四、解答题 | |||
| 17 | 0.85 | 判断等差数列 裂项相消法求和 利用an与sn关系求通项或项 | 问答题 |
| 18 | 0.65 | 正弦定理解三角形 正弦定理边角互化的应用 三角形面积公式及其应用 余弦定理解三角形 | 问答题 |
| 19 | 0.65 | 利用互斥事件的概率公式求概率 写出简单离散型随机变量分布列 求离散型随机变量的均值 | 应用题 |
| 20 | 0.65 | 证明线面垂直 线面垂直证明线线垂直 线面角的向量求法 | 问答题 |
| 21 | 0.4 | 数量积的坐标表示 求抛物线的轨迹方程 求抛物线的切线方程 根据韦达定理求参数 | 问答题 |
| 22 | 0.4 | 用导数判断或证明已知函数的单调性 利用导数证明不等式 利用导数研究函数的零点 | 问答题 |

 满足
满足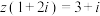 (
( 是虚数单位),则在复平面内
是虚数单位),则在复平面内 对应的点位于(
对应的点位于( ,
, 满足
满足 ,则
,则 与
与

