2024高三·全国·专题练习
1 . 已知 ,函数
,函数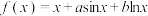 .
.
(1)当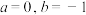 时,求
时,求 的单调区间;
的单调区间;
(2)当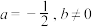 时,设
时,设 的导函数为
的导函数为 ,若
,若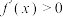 恒成立,求证:存在
恒成立,求证:存在 ,使得
,使得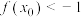 ;
;
(3)设 ,若存在
,若存在 ,使得
,使得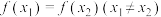 ,证明:
,证明: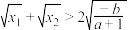 .
.
 ,函数
,函数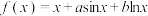 .
.(1)当
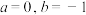 时,求
时,求 的单调区间;
的单调区间;(2)当
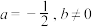 时,设
时,设 的导函数为
的导函数为 ,若
,若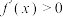 恒成立,求证:存在
恒成立,求证:存在 ,使得
,使得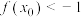 ;
;(3)设
 ,若存在
,若存在 ,使得
,使得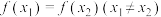 ,证明:
,证明: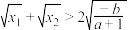 .
.
您最近一年使用:0次
2 . 已知圆C过点 ,
,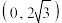 ,
, .
.
(1)求圆C的标准方程;
(2)若过点C且与x轴平行的直线与圆C交于点M,N,点P为直线 上的动点,直线PM,PN与圆C的另一个交点分别为E,F(EF与MN不重合),证明:直线EF过定点.
上的动点,直线PM,PN与圆C的另一个交点分别为E,F(EF与MN不重合),证明:直线EF过定点.
 ,
,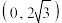 ,
, .
.(1)求圆C的标准方程;
(2)若过点C且与x轴平行的直线与圆C交于点M,N,点P为直线
 上的动点,直线PM,PN与圆C的另一个交点分别为E,F(EF与MN不重合),证明:直线EF过定点.
上的动点,直线PM,PN与圆C的另一个交点分别为E,F(EF与MN不重合),证明:直线EF过定点.
您最近一年使用:0次
名校
解题方法
3 . 函数极限是现代数学中非常重要的概念,函数 在
在 处的极限定义如下:
处的极限定义如下: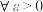 ,存在正数
,存在正数 ,当
,当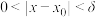 时,均有
时,均有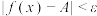 ,则称
,则称 在
在 处的极限为A,记为
处的极限为A,记为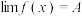 ,例如:
,例如: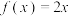 在
在 处的极限为2,理由是:
处的极限为2,理由是: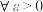 ,存在正数
,存在正数 ,当
,当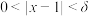 时,均有
时,均有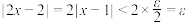 ,所以
,所以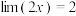 .已知函数
.已知函数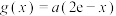 ,
,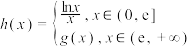 ,(
,( ,
, 为自然对数的底数).
为自然对数的底数).
(1)证明: 在
在 处的极限为
处的极限为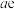 ;
;
(2)若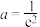 ,
, ,
, ,求
,求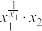 的最大值;
的最大值;
(3)若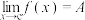 ,用函数极限的定义证明:
,用函数极限的定义证明: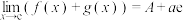 .
.
 在
在 处的极限定义如下:
处的极限定义如下: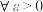 ,存在正数
,存在正数 ,当
,当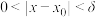 时,均有
时,均有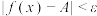 ,则称
,则称 在
在 处的极限为A,记为
处的极限为A,记为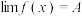 ,例如:
,例如: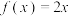 在
在 处的极限为2,理由是:
处的极限为2,理由是: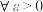 ,存在正数
,存在正数 ,当
,当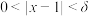 时,均有
时,均有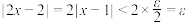 ,所以
,所以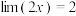 .已知函数
.已知函数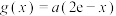 ,
,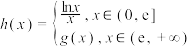 ,(
,( ,
, 为自然对数的底数).
为自然对数的底数).(1)证明:
 在
在 处的极限为
处的极限为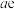 ;
;(2)若
 ,
, ,
, ,求
,求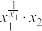 的最大值;
的最大值;(3)若
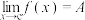 ,用函数极限的定义证明:
,用函数极限的定义证明: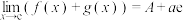 .
.
您最近一年使用:0次
4 . 已知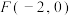 ,
,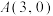 ,直线l:
,直线l: ,动点P到l的距离为d,满足
,动点P到l的距离为d,满足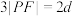 ,设点P的轨迹为C,过点F作直线
,设点P的轨迹为C,过点F作直线 ,交C于G,H两点,过点F作与
,交C于G,H两点,过点F作与 垂直的直线
垂直的直线 ,直线l与
,直线l与 交于点K,连接AG,AH,分别交直线l于M,N两点.
交于点K,连接AG,AH,分别交直线l于M,N两点.
(1)求C的方程;
(2)证明: ;
;
(3)记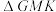 ,
,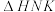 的面积分别为
的面积分别为 ,
, ,四边形AGKH的面积为
,四边形AGKH的面积为 ,求
,求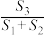 的范围.
的范围.
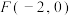 ,
,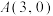 ,直线l:
,直线l: ,动点P到l的距离为d,满足
,动点P到l的距离为d,满足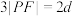 ,设点P的轨迹为C,过点F作直线
,设点P的轨迹为C,过点F作直线 ,交C于G,H两点,过点F作与
,交C于G,H两点,过点F作与 垂直的直线
垂直的直线 ,直线l与
,直线l与 交于点K,连接AG,AH,分别交直线l于M,N两点.
交于点K,连接AG,AH,分别交直线l于M,N两点.(1)求C的方程;
(2)证明:
 ;
;(3)记
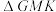 ,
,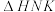 的面积分别为
的面积分别为 ,
, ,四边形AGKH的面积为
,四边形AGKH的面积为 ,求
,求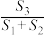 的范围.
的范围.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
5 . 已知函数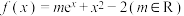 ,
, .
.
(1)若直线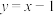 是函数
是函数 的图象的切线,求实数
的图象的切线,求实数 的值;
的值;
(2)当 时,证明:对于任意的
时,证明:对于任意的 ,不等式
,不等式 恒成立.
恒成立.
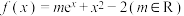 ,
, .
.(1)若直线
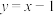 是函数
是函数 的图象的切线,求实数
的图象的切线,求实数 的值;
的值;(2)当
 时,证明:对于任意的
时,证明:对于任意的 ,不等式
,不等式 恒成立.
恒成立.
您最近一年使用:0次
2024高三下·全国·专题练习
6 . 已知函数 (
( ).
).
(1)求 的单调区间;
的单调区间;
(2)若函数 ,
, 是函数
是函数 的两个零点,证明:
的两个零点,证明: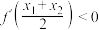 .
.
 (
( ).
).(1)求
 的单调区间;
的单调区间;(2)若函数
 ,
, 是函数
是函数 的两个零点,证明:
的两个零点,证明: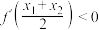 .
.
您最近一年使用:0次
名校
7 . 若数列 若满足递推关系
若满足递推关系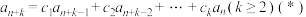 其中
其中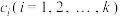 为常数,我们称该数列为k阶常系数齐次线性递推数列,并称方程
为常数,我们称该数列为k阶常系数齐次线性递推数列,并称方程 为递推关系式(*)的特征方程,该方程的根称为数列
为递推关系式(*)的特征方程,该方程的根称为数列 的特征根.我们有以下结论:对于k阶常系数齐次线性递推数列,若其不同的特征根为
的特征根.我们有以下结论:对于k阶常系数齐次线性递推数列,若其不同的特征根为 ,
, ,…,
,…, ,且特征根
,且特征根 的重数为
的重数为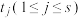 ,则数列
,则数列 的通项公式为
的通项公式为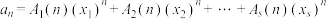
其中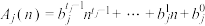 ,
,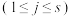 ,这里
,这里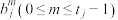 都是常数,它们由数列初始值可以确定.
都是常数,它们由数列初始值可以确定.
(1)若数列 满足
满足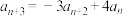 ,且
,且 ,
,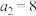 ,
, ,求数列
,求数列 的通项公式;
的通项公式;
(2)若数列 满足对于所有非负整数m,n(
满足对于所有非负整数m,n( ),
),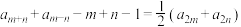 都成立,且
都成立,且 ,求数列
,求数列 的通项公式;
的通项公式;
(3)设边长为1的正六边形ABCDEF,O是六边形的中心,除了六边形的每一条边,我们还从点O到每个顶点连一条线段,共得到12条长度为1的线段,一条路径是指动点沿着上述线段(全部或部分)移动,始点终点均为点O的一条移动路线.求长度为2024的路径共有多少条?(注:根的重数就是方程中同样根的数量)
 若满足递推关系
若满足递推关系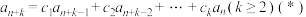 其中
其中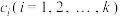 为常数,我们称该数列为k阶常系数齐次线性递推数列,并称方程
为常数,我们称该数列为k阶常系数齐次线性递推数列,并称方程 为递推关系式(*)的特征方程,该方程的根称为数列
为递推关系式(*)的特征方程,该方程的根称为数列 的特征根.我们有以下结论:对于k阶常系数齐次线性递推数列,若其不同的特征根为
的特征根.我们有以下结论:对于k阶常系数齐次线性递推数列,若其不同的特征根为 ,
, ,…,
,…, ,且特征根
,且特征根 的重数为
的重数为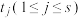 ,则数列
,则数列 的通项公式为
的通项公式为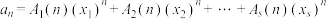
其中
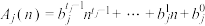 ,
,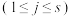 ,这里
,这里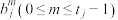 都是常数,它们由数列初始值可以确定.
都是常数,它们由数列初始值可以确定.(1)若数列
 满足
满足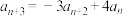 ,且
,且 ,
,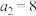 ,
, ,求数列
,求数列 的通项公式;
的通项公式;(2)若数列
 满足对于所有非负整数m,n(
满足对于所有非负整数m,n( ),
),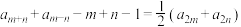 都成立,且
都成立,且 ,求数列
,求数列 的通项公式;
的通项公式;(3)设边长为1的正六边形ABCDEF,O是六边形的中心,除了六边形的每一条边,我们还从点O到每个顶点连一条线段,共得到12条长度为1的线段,一条路径是指动点沿着上述线段(全部或部分)移动,始点终点均为点O的一条移动路线.求长度为2024的路径共有多少条?(注:根的重数就是方程中同样根的数量)
您最近一年使用:0次
名校
8 . 极值的广义定义如下:如果一个函数在一点的一个邻域(包含该点的开区间)内处处都有确定的值,而以该点处的值为最大(小),这函数在该点处的值就是一个极大(小)值.
对于函数 ,设自变量x从
,设自变量x从 变化到
变化到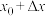 ,当
,当 ,
,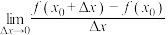 是一个确定的值,则称函数
是一个确定的值,则称函数 在点
在点 处右可导;当
处右可导;当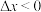 ,
,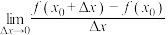 是一个确定的值,则称函数
是一个确定的值,则称函数 在点
在点 处左可导.当函数
处左可导.当函数 在点
在点 处既右可导也左可导且导数值相等,则称函数
处既右可导也左可导且导数值相等,则称函数 在点
在点 处可导.
处可导.
(1)请举出一个例子,说明该函数在某点处不可导,但是该点是该函数的极值点;
(2)已知函数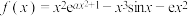 .
.
(ⅰ)求函数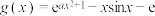 在
在 处的切线方程;
处的切线方程;
(ⅱ)若 为
为 的极小值点,求a的取值范围.
的极小值点,求a的取值范围.
对于函数
 ,设自变量x从
,设自变量x从 变化到
变化到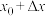 ,当
,当 ,
,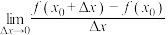 是一个确定的值,则称函数
是一个确定的值,则称函数 在点
在点 处右可导;当
处右可导;当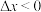 ,
,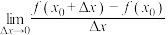 是一个确定的值,则称函数
是一个确定的值,则称函数 在点
在点 处左可导.当函数
处左可导.当函数 在点
在点 处既右可导也左可导且导数值相等,则称函数
处既右可导也左可导且导数值相等,则称函数 在点
在点 处可导.
处可导.(1)请举出一个例子,说明该函数在某点处不可导,但是该点是该函数的极值点;
(2)已知函数
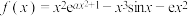 .
.(ⅰ)求函数
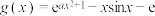 在
在 处的切线方程;
处的切线方程;(ⅱ)若
 为
为 的极小值点,求a的取值范围.
的极小值点,求a的取值范围.
您最近一年使用:0次
9 . 若数列 和
和 的项数均为
的项数均为 ,则将数列
,则将数列 和
和 的距离定义为
的距离定义为 .
.
(1)求数列1,3,5,6和数列2,3,10,7的距离;
(2)记A为满足递推关系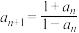 的所有数列
的所有数列 的集合,数列
的集合,数列 和
和 为A中的两个元素,且项数均为
为A中的两个元素,且项数均为 .若
.若 ,
, ,数列
,数列 和
和 的距离
的距离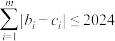 ,求m的最大值;
,求m的最大值;
(3)记S是所有7项数列 (其中
(其中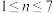 ,
, 或1)的集合,
或1)的集合,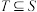 ,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
 和
和 的项数均为
的项数均为 ,则将数列
,则将数列 和
和 的距离定义为
的距离定义为 .
.(1)求数列1,3,5,6和数列2,3,10,7的距离;
(2)记A为满足递推关系
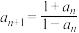 的所有数列
的所有数列 的集合,数列
的集合,数列 和
和 为A中的两个元素,且项数均为
为A中的两个元素,且项数均为 .若
.若 ,
, ,数列
,数列 和
和 的距离
的距离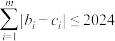 ,求m的最大值;
,求m的最大值;(3)记S是所有7项数列
 (其中
(其中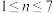 ,
, 或1)的集合,
或1)的集合,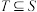 ,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
您最近一年使用:0次
10 . 已知函数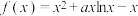
(1)当 时,求
时,求 的零点;
的零点;
(2)若 恰有两个极值点,求
恰有两个极值点,求 的取值范围.
的取值范围.
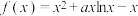
(1)当
 时,求
时,求 的零点;
的零点;(2)若
 恰有两个极值点,求
恰有两个极值点,求 的取值范围.
的取值范围.
您最近一年使用:0次



