2020届广东省汕头市金山中学高三下学期第三次模拟(6月) 数学(文)试题
广东
高三
三模
2020-08-02
1685次
整体难度:
适中
考查范围:
集合与常用逻辑用语、复数、平面解析几何、函数与导数、计数原理与概率统计、算法与框图、数列、空间向量与立体几何、三角函数与解三角形、平面向量、等式与不等式、坐标系与参数方程、不等式选讲
一、单选题 添加题型下试题
 所对应的点关于实轴对称的点为
所对应的点关于实轴对称的点为 ,则
,则 对应的复数为( )
对应的复数为( )A. | B. | C.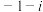 | D.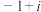 |
【知识点】 复数的除法运算解读 共轭复数的概念及计算解读
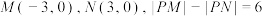 ,则动点
,则动点 的轨迹是( )
的轨迹是( )| A.一条射线 | B.双曲线右支 | C.双曲线 | D.双曲线左支 |
【知识点】 双曲线定义的理解
 为奇函数,当
为奇函数,当 时,
时, ,则
,则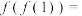 ( )
( )| A.-1 | B.-2 | C.1 | D.2 |
【知识点】 函数奇偶性的应用
 中,
中, ,则“
,则“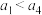 ”是“
”是“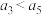 ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
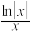 的图象大致形状是( )
的图象大致形状是( )A.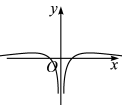 | B. |
C. | D.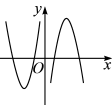 |
【知识点】 函数奇偶性的定义与判断解读 函数奇偶性的应用 函数图像的识别
| A.99 | B.131 | C.139 | D.141 |
 的首项
的首项 ,且满足
,且满足 ,则
,则 的最小的一项是
的最小的一项是A. | B.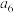 | C. | D.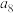 |
【知识点】 确定数列中的最大(小)项 累加法求数列通项

| A.40 | B.43 | C.46 | D.47 |
【知识点】 由三视图还原几何体
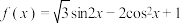 ,将
,将 的图象上的所有点的横坐标缩短到原来的
的图象上的所有点的横坐标缩短到原来的 ,纵坐标保持不变;再把所得图象向上平移
,纵坐标保持不变;再把所得图象向上平移 个单位长度,得到函数
个单位长度,得到函数 的图象,若
的图象,若 ,则
,则 的值可能为( )
的值可能为( )A.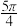 | B. | C. | D. |
 的左、右两个焦点分别为
的左、右两个焦点分别为 ,以线段
,以线段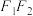 为直径的圆与双曲线的渐近线在第一象限的交点为
为直径的圆与双曲线的渐近线在第一象限的交点为 ,若
,若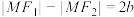 ,该双曲线的离心率为
,该双曲线的离心率为 ,则
,则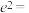
| A.2 | B.3 | C.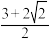 | D.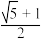 |
【知识点】 双曲线定义的理解 求双曲线的离心率或离心率的取值范围
二、填空题 添加题型下试题
 满足“勾3股4弦5”,其中“股”
满足“勾3股4弦5”,其中“股” ,
, 为“弦”
为“弦” 上一点(不含端点),且
上一点(不含端点),且 满足勾股定理,则
满足勾股定理,则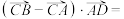
【知识点】 用定义求向量的数量积解读 已知模求数量积
 ,其中
,其中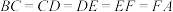 且
且 .则在圆内随机取一点,则此点取自六边形
.则在圆内随机取一点,则此点取自六边形 内的概率是
内的概率是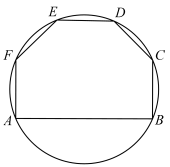
【知识点】 三角形面积公式及其应用解读 几何概型-面积型解读
 的四个顶点都在球
的四个顶点都在球 的表面上,
的表面上, 平面
平面 ,
,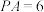 ,
,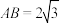 ,
,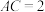 ,
,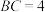 ,则球
,则球 的半径为
的半径为 是
是 的中点,过点
的中点,过点 作球
作球 的截面,则截面面积的最小值是
的截面,则截面面积的最小值是【知识点】 球的截面的性质及计算 多面体与球体内切外接问题
三、解答题 添加题型下试题
 内接于单位圆,且
内接于单位圆,且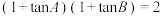 ,
,(1)求角

(2)求
 面积的最大值.
面积的最大值. .
.
(1)求证:AC1⊥B1C;
(2)若∠BCC1=60°,
 三棱锥A﹣BB1C的体积为
三棱锥A﹣BB1C的体积为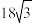 ,求三棱柱ABC﹣A1B1C1的表面积.
,求三棱柱ABC﹣A1B1C1的表面积.
【知识点】 棱柱表面积的有关计算 锥体体积的有关计算 线面垂直证明线线垂直
 :(单位:元/月)和购买人数
:(单位:元/月)和购买人数 (单位:万人)的关系如表:
(单位:万人)的关系如表:流量包的定价(元/月) | 30 | 35 | 40 | 45 | 50 |
购买人数(万人) | 18 | 14 | 10 | 8 | 5 |
 与
与 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;(2)①求出
 关于
关于 的回归方程;
的回归方程;②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:
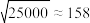 ,
, ,
,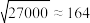 .
.参考公式:相关系数
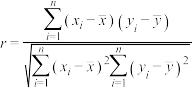 ,回归直线方程
,回归直线方程 ,其中
,其中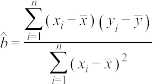 ,
, .
.
 :
: 上一点
上一点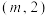 到其准线的距离为2.
到其准线的距离为2.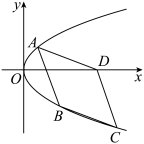
(1)求抛物线
 的方程;
的方程;(2)如图
 ,
, ,
, 为抛物线
为抛物线 上三个点,
上三个点,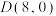 ,若四边形
,若四边形 为菱形,求四边形
为菱形,求四边形 的面积.
的面积.
(1)求f(x)在区间(0,π)的极值;
(2)证明:函数g(x)=f(x)﹣sinx﹣1在区间(﹣π,π)有且只有3个零点,且之和为0.
 为椭圆
为椭圆 任意一点,以坐标原点为极点,
任意一点,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为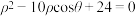 ,
, 为
为 上任意一点.
上任意一点.(1)写出
 的参数方程和
的参数方程和 的普通方程;
的普通方程;(2)求
 的最大值和最小值.
的最大值和最小值.
 满足
满足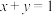 .
.(1)解关于
 的不等式
的不等式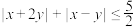 ;
;(2)证明:
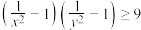 .
.
【知识点】 利用基本不等式证明不等式解读 公式法解绝对值不等式
试卷分析
导出试卷题型(共 23题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 列举法表示集合 交集的概念及运算 | |
| 2 | 0.85 | 复数的除法运算 共轭复数的概念及计算 | |
| 3 | 0.94 | 双曲线定义的理解 | |
| 4 | 0.85 | 函数奇偶性的应用 | |
| 5 | 0.85 | 几何概型-长度型 读懂条件语句的功能 根据条件语句计算输入、输出值 | |
| 6 | 0.85 | 充分条件的判定及性质 必要条件的判定及性质 等比数列通项公式的基本量计算 | |
| 7 | 0.65 | 函数奇偶性的定义与判断 函数奇偶性的应用 函数图像的识别 | |
| 8 | 0.85 | 递推数列的实际应用 数列新定义 | |
| 9 | 0.65 | 确定数列中的最大(小)项 累加法求数列通项 | |
| 10 | 0.65 | 由三视图还原几何体 | |
| 11 | 0.65 | 求含sinx(型)函数的值域和最值 求正弦(型)函数的最小正周期 求图象变化前(后)的解析式 三角恒等变换的实际应用 | |
| 12 | 0.4 | 双曲线定义的理解 求双曲线的离心率或离心率的取值范围 | |
| 二、填空题 | |||
| 13 | 0.85 | 用定义求向量的数量积 已知模求数量积 | 单空题 |
| 14 | 0.65 | 三角函数的化简、求值——诱导公式 二倍角的余弦公式 给值求值型问题 | 单空题 |
| 15 | 0.65 | 三角形面积公式及其应用 几何概型-面积型 | 单空题 |
| 16 | 0.4 | 球的截面的性质及计算 多面体与球体内切外接问题 | 单空题 |
| 三、解答题 | |||
| 17 | 0.65 | 三角形面积公式及其应用 余弦定理解三角形 基本(均值)不等式的应用 | 问答题 |
| 18 | 0.65 | 棱柱表面积的有关计算 锥体体积的有关计算 线面垂直证明线线垂直 | 证明题 |
| 19 | 0.85 | 用回归直线方程对总体进行估计 求回归直线方程 相关系数的计算 | 问答题 |
| 20 | 0.4 | 根据抛物线上的点求标准方程 抛物线中的三角形或四边形面积问题 | 问答题 |
| 21 | 0.4 | 利用导数求函数的单调区间(不含参) 求已知函数的极值 利用导数研究函数的零点 | 证明题 |
| 22 | 0.65 | 极坐标与直角坐标的互化 椭圆的参数方程 利用圆锥曲线的参数方程求最值问题 | 问答题 |
| 23 | 0.65 | 利用基本不等式证明不等式 公式法解绝对值不等式 | 问答题 |

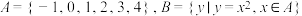 ,则
,则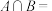 (
(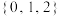
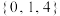
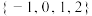
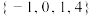
 内的均匀随机函数,则计算机执行下列程序后,输出的
内的均匀随机函数,则计算机执行下列程序后,输出的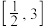 内的概率为
内的概率为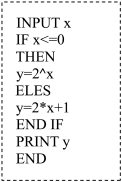

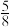
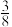
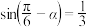 ,则
,则