名校
1 . 二次函数 最小值为
最小值为 ,且关于
,且关于 对称,又
对称,又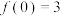 .
.
(1)求 的解析式;
的解析式;
(2)在区间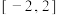 上,
上, 的图象恒在
的图象恒在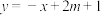 图象的下方,试确定实数
图象的下方,试确定实数 的取值范围;
的取值范围;
(3)求函数 在区间
在区间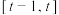 上的最小值
上的最小值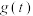 .
.
 最小值为
最小值为 ,且关于
,且关于 对称,又
对称,又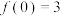 .
.(1)求
 的解析式;
的解析式;(2)在区间
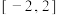 上,
上, 的图象恒在
的图象恒在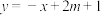 图象的下方,试确定实数
图象的下方,试确定实数 的取值范围;
的取值范围;(3)求函数
 在区间
在区间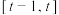 上的最小值
上的最小值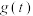 .
.
您最近一年使用:0次
2024-09-08更新
|
1309次组卷
|
4卷引用:吉林省吉林市第四中学2024-2025学年高一上学期9月月考数学试卷
名校
解题方法
2 . 已知数列 的前
的前 项和为
项和为 ,且
,且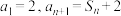 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设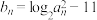 ,求数列
,求数列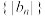 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,且
,且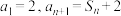 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
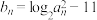 ,求数列
,求数列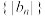 的前
的前 项和
项和 .
.
您最近一年使用:0次
2024-09-04更新
|
2176次组卷
|
8卷引用:吉林省通化市梅河口市第五中学2025届高三上学期10月月考数学试题
名校
解题方法
3 . 已知椭圆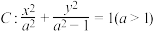 的左、右焦点分别为
的左、右焦点分别为 ,
, ,A,B两点均在C上,且
,A,B两点均在C上,且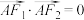 ,
, .
.
(1)若 ,求C的方程;
,求C的方程;
(2)若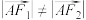 ,直线AB与y轴交于点P,且
,直线AB与y轴交于点P,且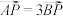 ,求四边形AF1BF2的周长.
,求四边形AF1BF2的周长.
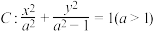 的左、右焦点分别为
的左、右焦点分别为 ,
, ,A,B两点均在C上,且
,A,B两点均在C上,且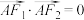 ,
, .
.(1)若
 ,求C的方程;
,求C的方程;(2)若
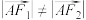 ,直线AB与y轴交于点P,且
,直线AB与y轴交于点P,且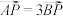 ,求四边形AF1BF2的周长.
,求四边形AF1BF2的周长.
您最近一年使用:0次
昨日更新
|
182次组卷
|
3卷引用:吉林省通化市集安市第一中学2024-2025学年高二上学期期中考试数学试题
名校
解题方法
4 . 已知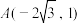 是抛物线
是抛物线 上的一点.
上的一点.
(1)求 的焦点坐标与准线方程;
的焦点坐标与准线方程;
(2)若直线 经过
经过 的焦点,且与
的焦点,且与 交于
交于 两点,求
两点,求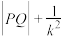 的最小值.
的最小值.
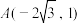 是抛物线
是抛物线 上的一点.
上的一点.(1)求
 的焦点坐标与准线方程;
的焦点坐标与准线方程;(2)若直线
 经过
经过 的焦点,且与
的焦点,且与 交于
交于 两点,求
两点,求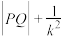 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
5 . 求符合下列条件的双曲线的标准方程:
(1)焦点在 轴上,实轴长为8,离心率为
轴上,实轴长为8,离心率为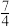 ;
;
(2)焦点在 轴上,焦距为
轴上,焦距为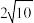 ,渐近线方程为
,渐近线方程为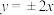 .
.
(1)焦点在
 轴上,实轴长为8,离心率为
轴上,实轴长为8,离心率为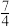 ;
;(2)焦点在
 轴上,焦距为
轴上,焦距为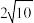 ,渐近线方程为
,渐近线方程为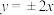 .
.
您最近一年使用:0次
昨日更新
|
645次组卷
|
3卷引用:吉林省八校2024-2025学年高二上学期10月期中考试数学试题
名校
解题方法
6 . 若正数x,y满足 ,
,
(1)求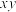 的最小值.
的最小值.
(2)求 的最小值.
的最小值.
 ,
,(1)求
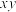 的最小值.
的最小值.(2)求
 的最小值.
的最小值.
您最近一年使用:0次
昨日更新
|
381次组卷
|
2卷引用:吉林省长春市第八中学2024-2025学年高一上学期第一次月考数学试题
解题方法
7 . 已知 ,
, 分别为函数
分别为函数 图象上相邻的最高点和最低点,
图象上相邻的最高点和最低点,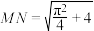 ,将函数
,将函数 的图象向左平移
的图象向左平移 个单位长度后得到函数
个单位长度后得到函数 的图象,
的图象, 为奇函数.
为奇函数.
(1)求函数 的解析式;
的解析式;
(2)在 中,角
中,角 的对边分别为
的对边分别为 ,若
,若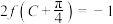 ,
,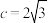 ,
, ,求
,求 的面积.
的面积.
 ,
, 分别为函数
分别为函数 图象上相邻的最高点和最低点,
图象上相邻的最高点和最低点,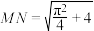 ,将函数
,将函数 的图象向左平移
的图象向左平移 个单位长度后得到函数
个单位长度后得到函数 的图象,
的图象, 为奇函数.
为奇函数.(1)求函数
 的解析式;
的解析式;(2)在
 中,角
中,角 的对边分别为
的对边分别为 ,若
,若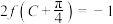 ,
,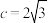 ,
, ,求
,求 的面积.
的面积.
您最近一年使用:0次
昨日更新
|
91次组卷
|
2卷引用:吉林省松原市长岭县第二中学2024-2025学年高三上学期第二次月考数学试卷
名校
8 . 已知函数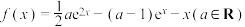 .
.
(1)当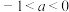 时,求
时,求 的单调区间;
的单调区间;
(2)若 在其定义域内不存在极值,求实数
在其定义域内不存在极值,求实数 的值.
的值.
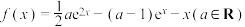 .
.(1)当
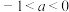 时,求
时,求 的单调区间;
的单调区间;(2)若
 在其定义域内不存在极值,求实数
在其定义域内不存在极值,求实数 的值.
的值.
您最近一年使用:0次
昨日更新
|
70次组卷
|
2卷引用:吉林省通化市梅河口市第五中学2025届高三上学期11月期中考试数学试题
名校
解题方法
9 . (1)在平面直角坐标系 中,已知动点
中,已知动点 到点
到点 的距离是到直线
的距离是到直线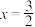 的距离的
的距离的 倍.求点
倍.求点 的轨迹方程;
的轨迹方程;
(2)若动圆 与圆
与圆 、圆
、圆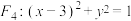 都外切.求动圆圆心
都外切.求动圆圆心 的轨迹方程.
的轨迹方程.
 中,已知动点
中,已知动点 到点
到点 的距离是到直线
的距离是到直线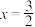 的距离的
的距离的 倍.求点
倍.求点 的轨迹方程;
的轨迹方程;(2)若动圆
 与圆
与圆 、圆
、圆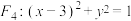 都外切.求动圆圆心
都外切.求动圆圆心 的轨迹方程.
的轨迹方程.
您最近一年使用:0次
名校
10 . 已知椭圆 的离心率为
的离心率为 ,点
,点 是椭圆上一点,点
是椭圆上一点,点 ,
, 分别是椭圆的左、右焦点,且
分别是椭圆的左、右焦点,且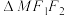 的周长为
的周长为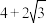 .
.
(1)求椭圆 的方程;
的方程;
(2)点 在椭圆上,且
在椭圆上,且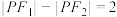 ,求
,求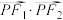 的值.
的值.
 的离心率为
的离心率为 ,点
,点 是椭圆上一点,点
是椭圆上一点,点 ,
, 分别是椭圆的左、右焦点,且
分别是椭圆的左、右焦点,且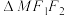 的周长为
的周长为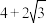 .
.(1)求椭圆
 的方程;
的方程;(2)点
 在椭圆上,且
在椭圆上,且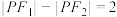 ,求
,求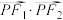 的值.
的值.
您最近一年使用:0次



